订阅用Mathematica学习微分几何——空间曲线初步
来源：网络收集 点击： 时间：2024-07-24三维空间曲线r的密切平面的方程：
r:={x,y,z}
p={x,y,z};
Det,r,r}]==0
圆柱螺旋线的密切平面方程是：
r := {Cos, Sin, t}
p = {x, y, z};
Det, r, r}] == 0
2/6空间曲线的逗留点：
如果Cross,r]==0，那么t就是这条曲线的逗留点。
可以证明圆柱螺旋线上面的所有点都不是逗留点：
r := {Cos, Sin, t}
Cross, r]
Cross, r].Cross, r]
3/6求圆柱螺旋线r:={Cos,Sin,t}在点｛1，0，0｝点的密切平面的方程。
稍微计算一下可知，此时t=0，
r := {Cos, Sin, t}
p = {x, y, z};
Det, r, r}] == 0 // Simplify // TraditionalForm
% /. t - 0
结果答案很简单，就是平面y==z
4/6给出曲线的自然参数方程r，那么它的单位切向量是：
α=D,s]
曲线的主法向量是：
β=D,{s,2}]/(D,{s,2}].D,{s,2}])
曲线的副法向量为：
γ=Cross
以圆柱螺旋线为例，整体代码是：
r := {Cos], Sin], s/Sqrt}
\ = r // Simplify
\ = r/(Sqrt.r]) // Simplify
\ = Cross, \]
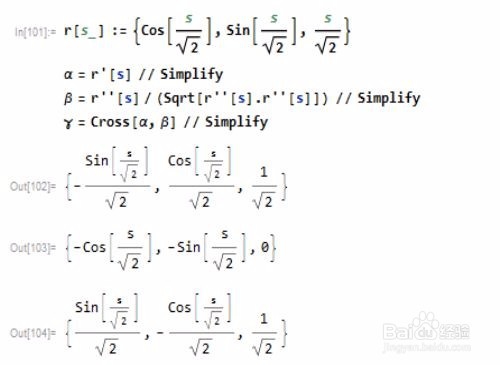5/6自然参数方程条件下，密切平面的方程是：
r:={x,y,z}
p={x,y,z};
Det==0
法平面的方程是：
(p-γ).α==0
从切平面的方程是：
(p-γ).β==0
以圆柱螺旋线为例：
r := {Cos], Sin], s/Sqrt}
\ = r // Simplify;
\ = r/(Sqrt.r]) // Simplify;
\ = Cross, \] // Simplify;
p = {x, y, z};
Det, \, \}] == 0 // Simplify
(p - \).\ == 0 // Simplify
(p - \).\ == 0 // Simplify
6/6对于曲线的一般参数方程r，有 ：
r:={Cos,Sin,t}
α=r/Sqrt.r]//Simplify
β=Cross,r]/Sqrt,r].Cross,r]]//Simplify
γ=((r.r) r-(r.r) r)/(Sqrt.r] Sqrt,r].Cross ,r]])//Simplify
注意事项就写到这吧！
MATHEMATICA微分几何版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_1002257.html
