本经验介绍含-α诱导类型三角函数的不定积分，即求∫sin(-α)dα，∫cos(-α)dα，∫tan(-α)dα，∫cot(-α)dα，∫sec(-α)dα，∫csc(-α)dα的步骤。工具/原料more三角函数基本知识 不定积分基本知识1.含-α的诱导公式1/2分步阅读

sin(-α)=-sin α

cos(-α)=cos α

tan(-α)=-tan α

cot(-α)=-cot α

sec(-α)=sec α

csc(-α)=-csc α

2/2

图例解析如下：

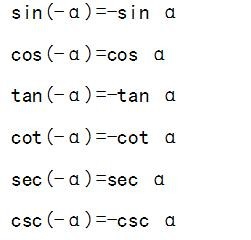2.sin(-α)dα1/2

∫sin(-α)dα

=-∫sin(-α)d(-α)

=cos(-α)+c

=cosα+c

2/2

图例解析如下：

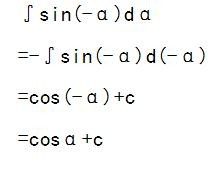3.cos(-α)dα1/2

∫cos(-α)dα

=-∫cos(-α)d(-α)

=-sin(-α)+c

=sinα+c

2/2

图例解析如下：

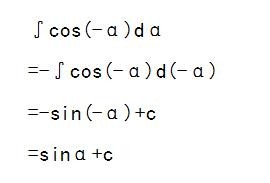4.tan(-α)dα1/2

∫tan(-α)dα

=-∫tan(-α)d(-α)

=-∫

=∫d cos(-α)/cos(-α)

=ln|cos(-α)|+c

=ln|cosα|+c

2/2

图例解析如下：

5.cot(-α)dα1/2

∫cot(-α)dα

=-∫cot(-α)d(-α)

=-∫

=-∫d sin(-α)/sin(-α)

=-ln|sin(-α)|+c

=-ln|sinα|+c

2/2

图例解析如下：

6.sec(-α)dα1/2

∫sec(-α)dα

=-∫sec(-α)dα

=-∫d(-α)/ cos(-α)

=-∫cos(-α)d(-α)/ ^2

=-∫dsin(-α)/

=-(1/2)

=-(1/2)ln{/ }+c

=-(1/2)ln+c

=-(1/2)ln+c

=-ln|(1+sin(-α))/cos(-α)|+c

=-ln|(1-sinα)/cosα|+c

=-ln|secα-tanα|+c

2/2

图例解析如下：

7.csc(-α)dα1/2

∫csc(-α)dα

=-∫csc(-α)d(-α)

=-∫d(-α)/ sin(-α)

=-∫sin(-α)d(-α)/ ^2

=∫dcos(-α)/

=∫dcos(-α)/

=(1/2)

=(1/2)ln+c

=(1/2)ln+c

=ln|(1+cos(-α))/sin(-α)|+c

=ln|(1+cosα)/sinα|+c

=ln|cscα+cota|+c

2/2

图例解析如下：

函数