以双曲线方程x^2/4^2-y^2/3^2=1和直线方程y=1/2*x+1为例，利用MATLAB求两者的交点，并绘制双曲线、直线和交点的图像。MATLAB提供了函数solve（）求方程组的解，这里将用其求双曲线和直线的交点。另外，MATLAB提供的ezplot（）可以快速绘制符号表达式的图像。工具/原料moreMATLABsolve双曲线直线方法/步骤1/5分步阅读

第一，利用MATLAB求下图双曲线方程x^2/4^2-y^2/3^2=1和直线方程y=1/2*x+1的交点。

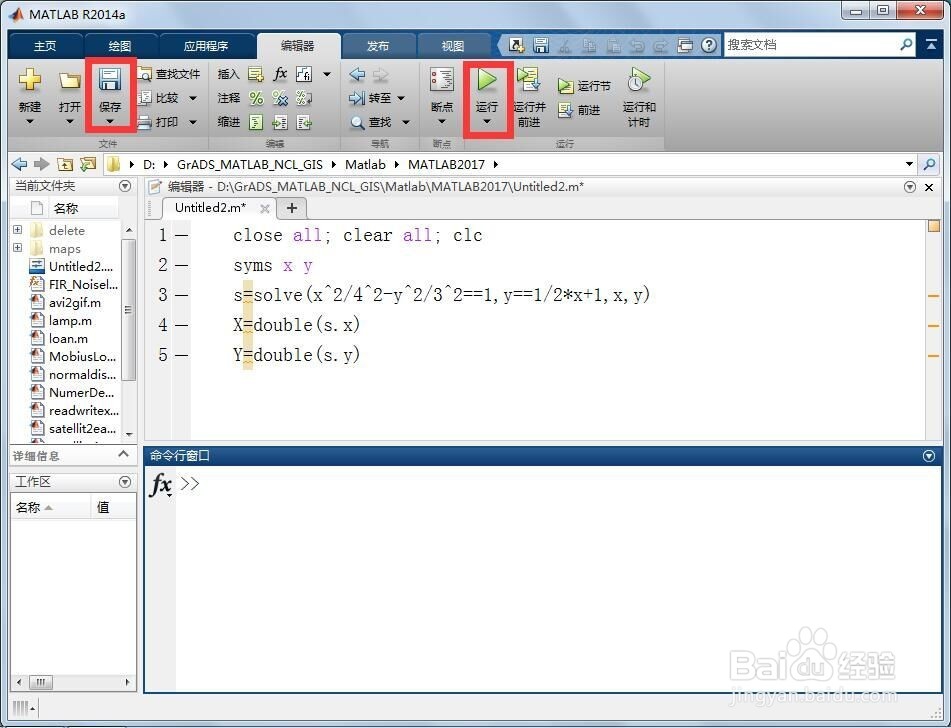
2/5

第二，启动MATLAB，新建脚本（Ctrl+N），在脚本编辑区输入如下代码：

close all; clear all; clc

syms x y

s=solve(x^2/4^2-y^2/3^2==1,y==1/2*x+1,x,y)

X=double(s.x)

Y=double(s.y)

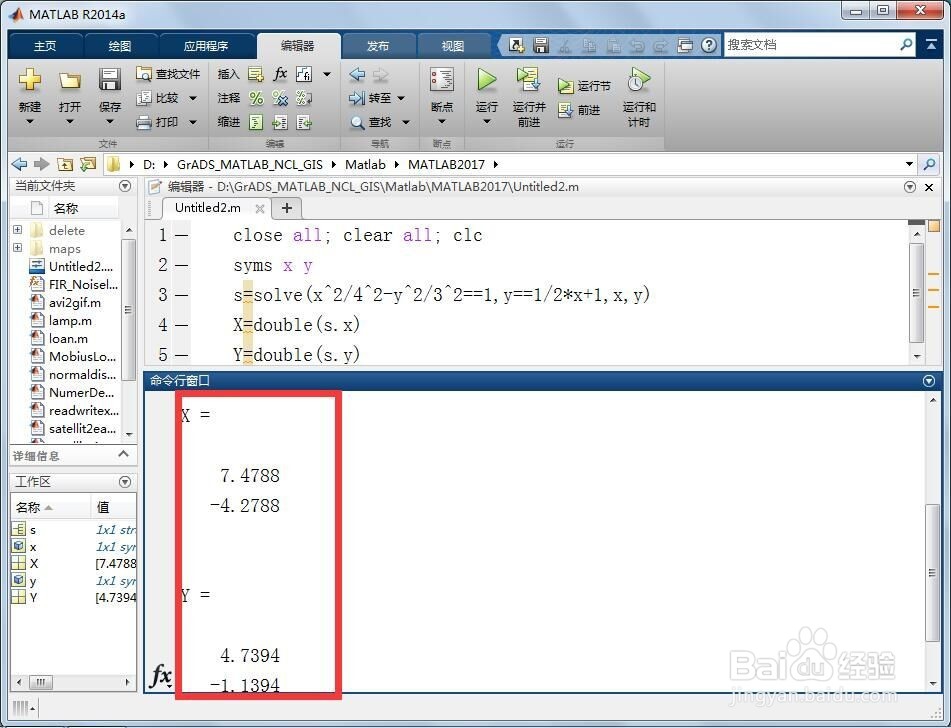
3/5

第三，保存和运行上述代码，在命令行窗口返回如下结果：

X =

7.4788

-4.2788

Y =

4.7394

-1.1394

也就是说，双曲线方程x^2/4^2-y^2/3^2=1和直线方程y=1/2*x+1有两个交点，分别为(7.4788, 4.7394)和(-4.2788, -1.1394)。

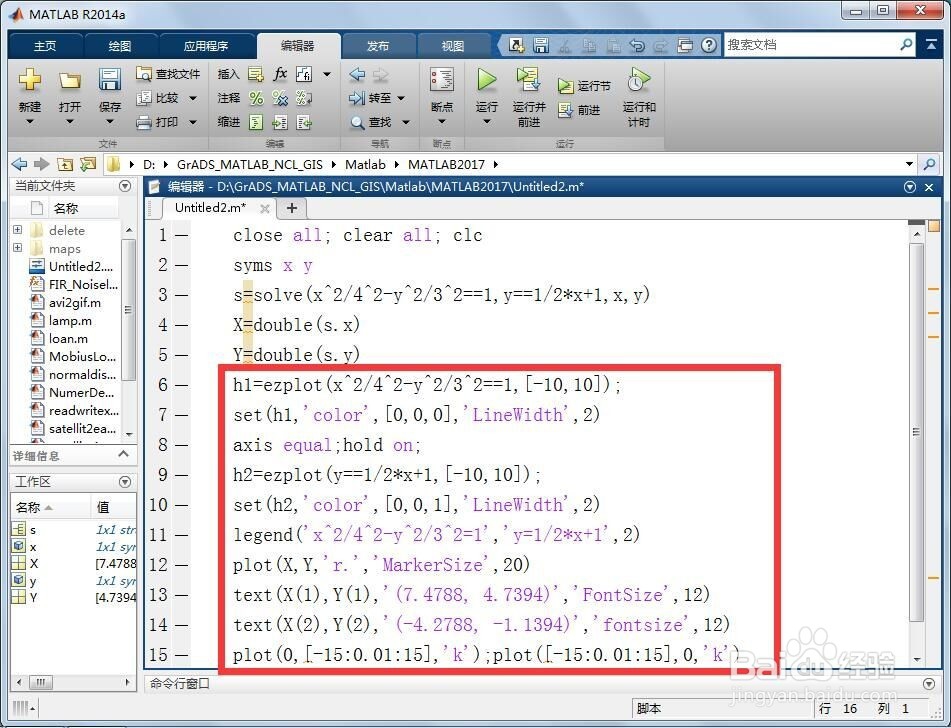
4/5

第四，在第二步脚本的基础上，绘制出双曲线方程、直线方程的图像，并标出它们的两个交点。只需在脚本编辑区接着输入如下代码：

h1=ezplot(x^2/4^2-y^2/3^2==1,);

set(h1,color,,LineWidth,2)

axis equal;hold on;

h2=ezplot(y==1/2*x+1,);

set(h2,color,,LineWidth,2)

legend(x^2/4^2-y^2/3^2=1,y=1/2*x+1,2)

plot(X,Y,r.,MarkerSize,20)

text(X(1),Y(1),(7.4788, 4.7394),FontSize,12)

text(X(2),Y(2),(-4.2788, -1.1394),fontsize,12)

plot(0,,k);plot(,0,k)

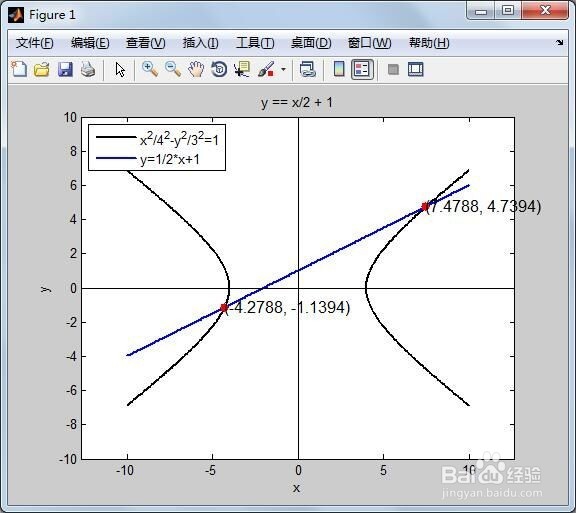
5/5

第五，保存和运行上述改进后的脚本，得到双曲线方程x^2/4^2-y^2/3^2=1和直线方程y=1/2*x+1的图像，并且标出了它们的两个交点(7.4788, 4.7394)和(-4.2788, -1.1394)。

注意事项

双曲线方程x^2/a^2-y^2/b^2=1，其渐近线方程为y=b/a*x和y=-b/a*x。

渐近线y=b/a*x和y=-b/a*x这两条直线方程与双曲线方程是没有交点的，其他直线方程与双曲线方程至少有一个交点。

MATLABSOLVE双曲线直线渐近线