在matlab中如何进行特征值的分解?
来源:网络收集 点击: 时间:2024-08-04【导读】:
学习。工具/原料morematlab方法/步骤1/7分步阅读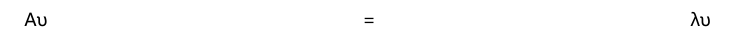 2/7
2/7 3/7
3/7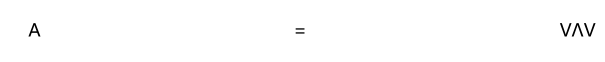 4/7
4/7 5/7
5/7 6/7
6/7 7/7
7/7
方阵 A 的特征值和特征向量分别为满足以下条件的标量 λ 和非零向量 υ
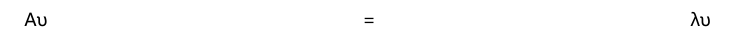 2/7
2/7对于对角矩阵的对角线上的特征值 Λ 以及构成矩阵列的对应特征向量 V,公式为
 3/7
3/7如果 V 是非奇异的,这将变为特征值分解。
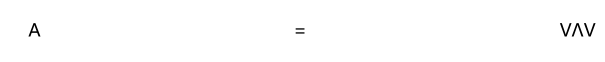 4/7
4/7微分方程 dx/dt = Ax 的系数矩阵就是一个很好的示例:
 5/7
5/7此方程的解用矩阵指数 x(t) = e tA x(0) 表示。语句
lambda = eig(A)
生成包含 A 的特征值的列向量。对于该矩阵,这些特征值为复数:
 6/7
6/7每个特征值的实部都为负数,因此随着 t 的增加,e λt 将会接近零。两个特征值 ±ω 的非零虚部为微分方程的解提供了振动分量 sin(ωt)。
使用这两个输出参数,eig 便可以计算特征向量并将特征值存储在对角矩阵中:
= eig(A)
 7/7
7/7第一个特征向量为实数,另外两个向量互为共轭复数。所有三个向量都归一化为具有等于 1 的欧几里德长度 norm(v,2)。
矩阵 V*D*inv(V)(可更简洁地写为 V*D/V)位于 A 的舍入误差界限内。inv(V)*A*V 或 V\A*V 都在D 的舍入误差界限内。
MATLAB版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_1059150.html
上一篇:手机怎么同时使用两个微信号?微信能不能双开?
下一篇:抖音开播公告怎么弄
 订阅
订阅