我们完全可以利用手头现有的一些数据加上某种概率分布随机产生的数据, 生成较大的测试数据集,又或许数据集合过大, 那也可以采用重新抽样的形式类进行部分数据的提取.函数 RandomReal、RandomInteger 和 RandomComplex 生成均匀分布的随机数. RandomVariate 生成内置分布的数. RandomPrime 生成一定范围内的素数. 函数 RandomChoice 和 RandomSample 从一列值中进行放回或无放回抽样. 元素的权重可以相同也可以不同.方法/步骤1/5分步阅读

有一点我们很有必要知道的技巧就是提高生成随机数据的效率, 如同下例所示那样, RandomReal 等函数可以一次性生成多组的数据集合, 而不需要用 Table 来产生哪些随机的数据, 显而易见, 第一种方式所花费的时间是最少的.

2/5

再来看一个蒙特卡洛方法求 \ 的近似的例子, 基本的思想就是在矩形内, 随机生成大量的坐标, 统计落在单位圆内的点数, 然后计算落在园内的点与总点数的比值, 就可以近似的求出 pi 值. 第一步, 我们首先在由{-1,-1} 和 {1,1}的正方形内生成10,000个点, 再来统计落在单位圆内外的点, 这里我用了一个 Sow 函数, 同时给这两类的点加上了标签, 可以用于以后的可视化. 看下图的所示, 分成了两大类: 单位圆内的红点和单位圆外的黑点.

3/5

怎么取出这两大类点的坐标呢? 我这里用了替换的操作来完成这一项任务, 当然用 Part 也完全Ok的. 如图所示, 两个结果完全一致.

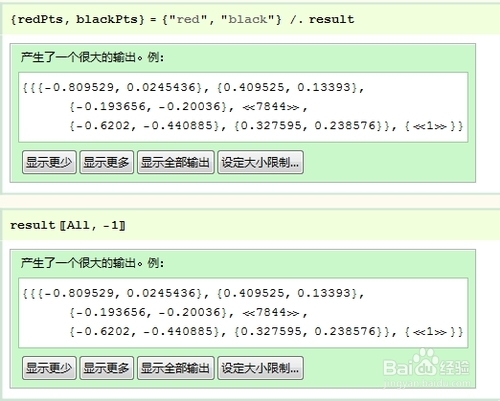4/5

下面我们把图形绘制处理啊, 在计算圆的面积, 所得结果当然和 3.1415.... 是有误差的.

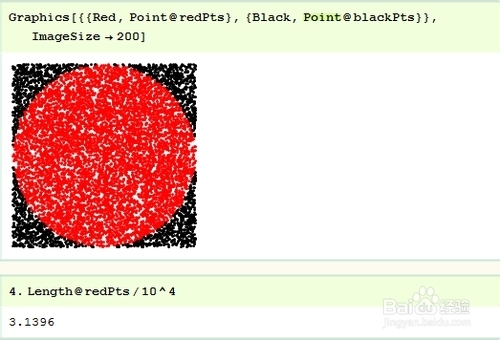5/5

我们再来一次实验, 增大生成的点数, 看看, 随着点的增大, 是否会越来越趋近于 pi . 并且这里还有提醒大家的是, 最好通过手动设定种子, 就可以每次随机的重现结果. 这种方法有助于我们以后的调试, 和让别人重复我们的结果.

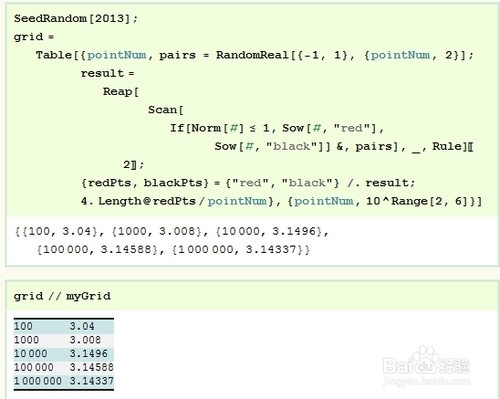注意事项

在做可视化的时候, 用随机的情况是随处可见, 但在产生一个随机数据之前, 记得设定一个随机的种子, 这样就可以反复重现刚才的结果.nbsp;

随机数