【抽象代数】正四面体群的三维矩阵表示
来源:网络收集 点击: 时间:2024-02-23【导读】:
本文,介绍一下正四面体的对称群的三维表示。工具/原料more电脑Mathematica方法/步骤1/6分步阅读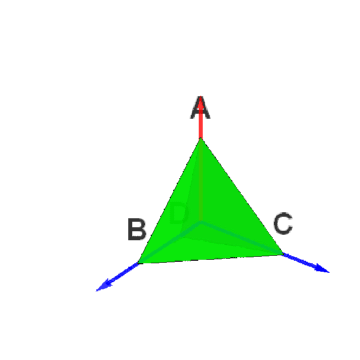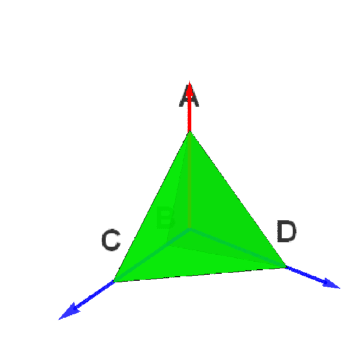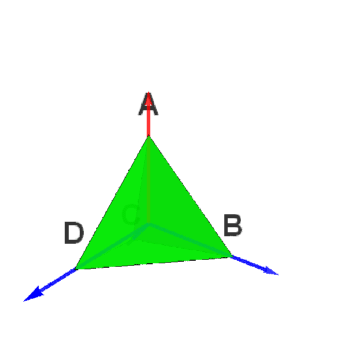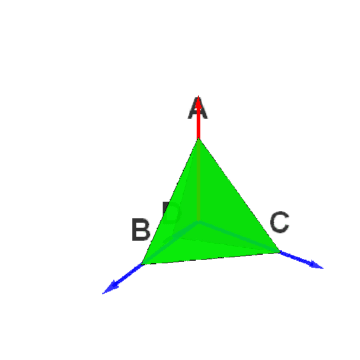 2/6
2/6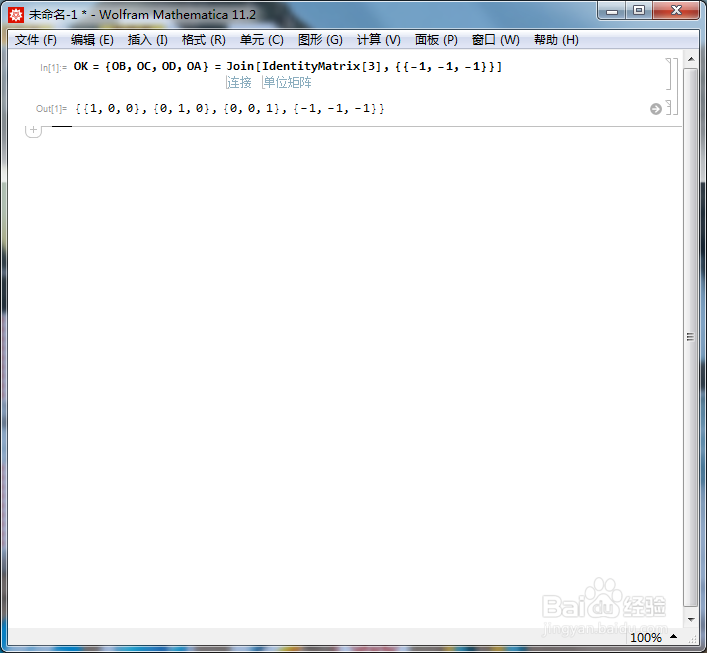 3/6
3/6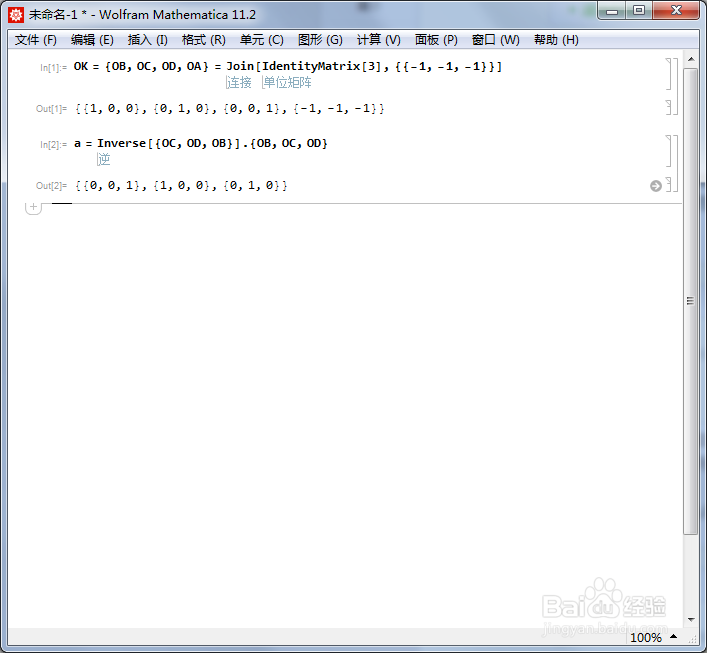 4/6
4/6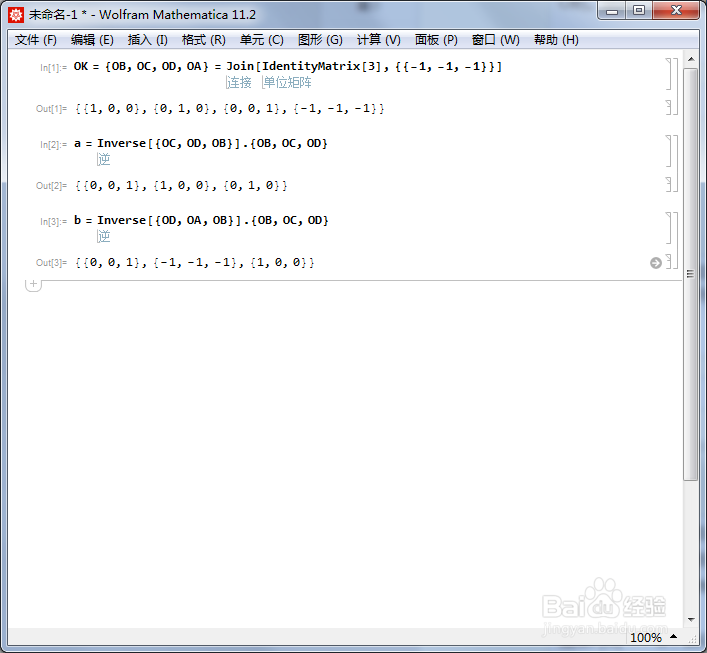 5/6
5/6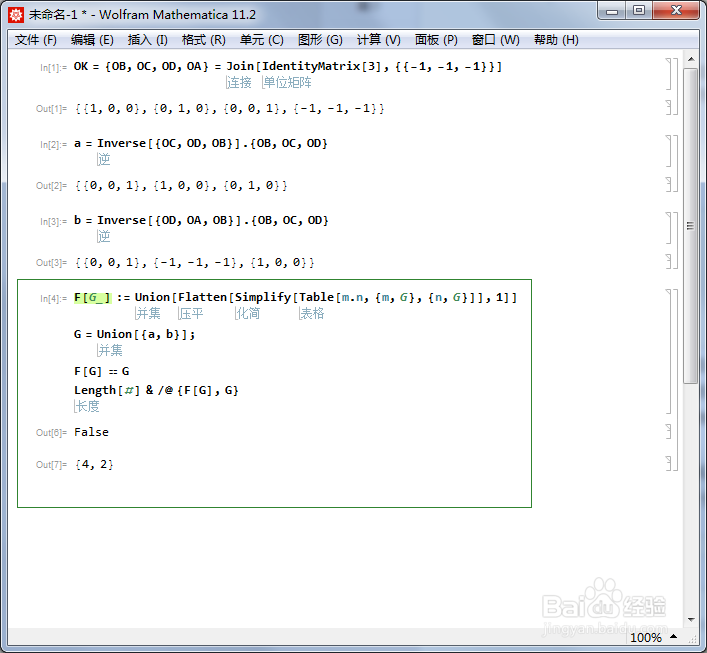 6/6
6/6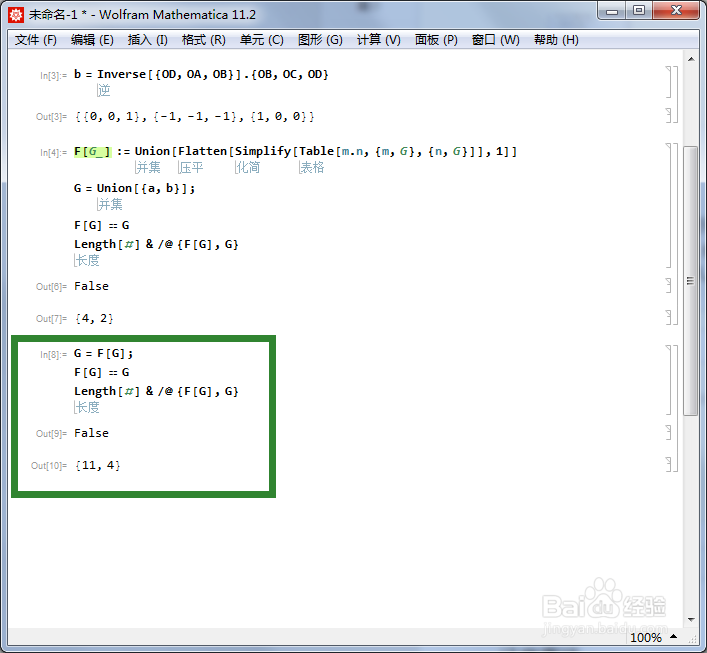
正四面体群最直接的表示,就是群元素作用于正四面体。
 2/6
2/6如果O为正四面体的中心,选择向量集合{OB、OC、OD}作为三维空间的基,那么,点B的坐标就可以写为:{1,0,0},点C的坐标就可以写为:{0,1,0},点D的坐标就可以写为:{0,0,1}。
进而,点A的坐标可以写为{-1,-1,-1},这是因为O=(A+B+C+D)/4。
 3/6
3/6以OA为旋转轴,旋转120°,这个变换记为a,它把{OB,OC,OD}变成了{OC,OD,OB}。因此,a对应的旋转矩阵可以表示为:
 4/6
4/6设AC的中点为X,BD的中点为Y,以XY为旋转轴旋转180°,把这个变换记为b,它把{OB,OC,OD}变成了{OD,OA,OB}。因此,b对应的旋转矩阵可以表示为:
 5/6
5/6这样,a和b就可以生成整个正四面体群。
先用集合{a,b}作乘法表,并查看乘法表里面的元素是否能够成为一个群:
F := Union], 1]]
G = Union;
如果F == G,则G为群。
但是此时,F四个元素,而G有两个元素,因此G不是群。
 6/6
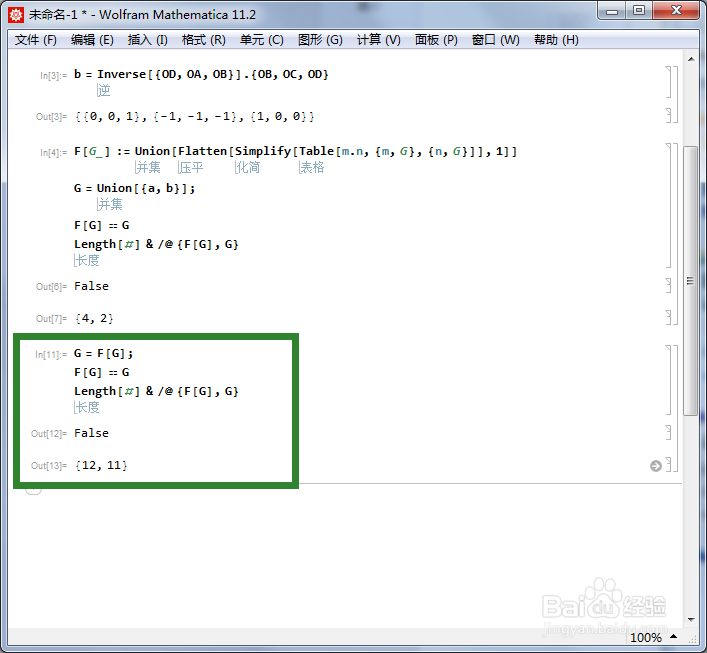
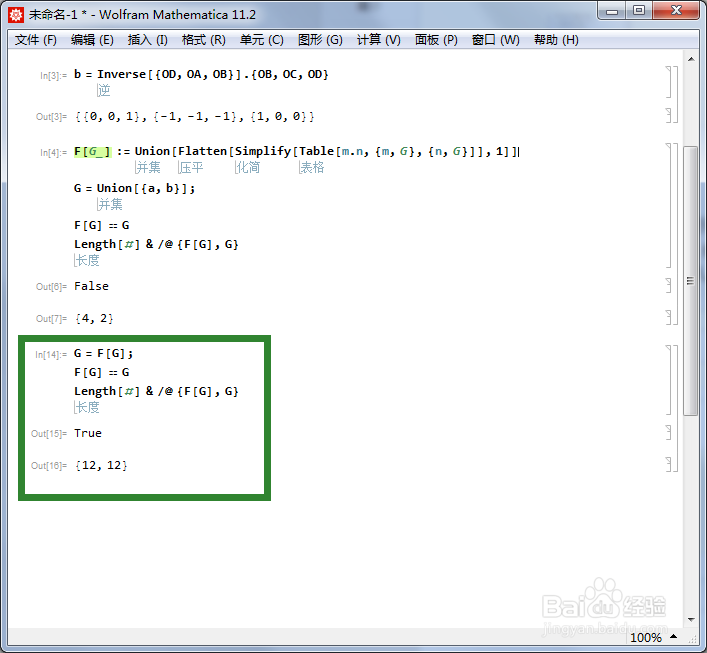
6/6用F代替G。
G = F;
F == G
Length /@ {F, G}
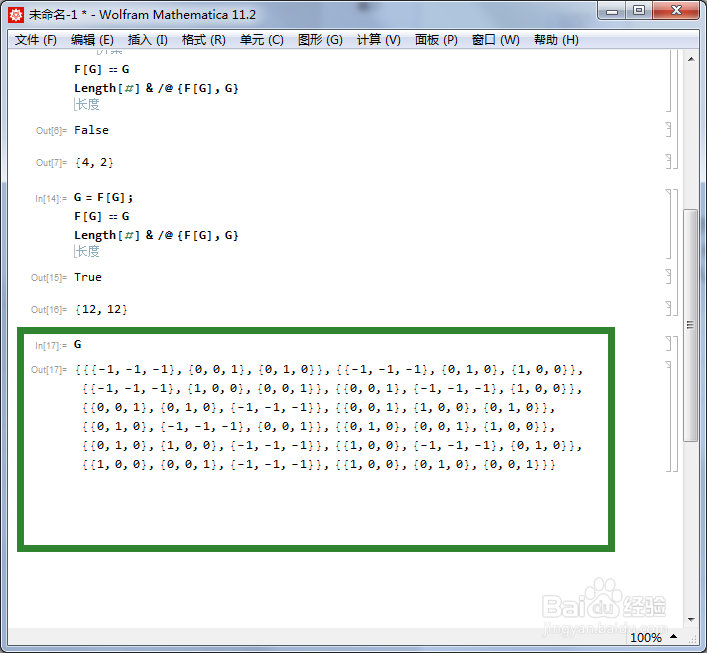
这个程序运行三次,终于得到F == G,此时G有12个元素。这恰好是正四面体群的一个三维表示。




版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_110173.html
上一篇:婴儿棉裤的裁剪及制作方法
下一篇:怎样设置高德导航时详细播报?
 订阅
订阅