反正切函数的导数
来源:网络收集 点击: 时间:2024-08-16【导读】:
很多人不知道反正切函数的导数怎么求?今天我教大家一种反正切函数的导数求法。具体如下。工具/原料more反正切函数的知识纸和笔方法/步骤1/4分步阅读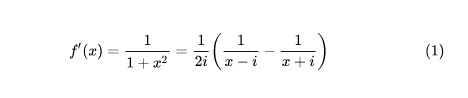
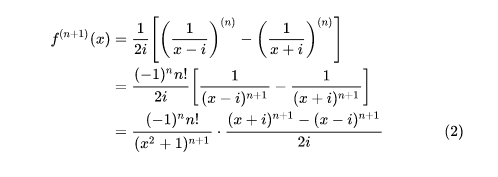 2/4
2/4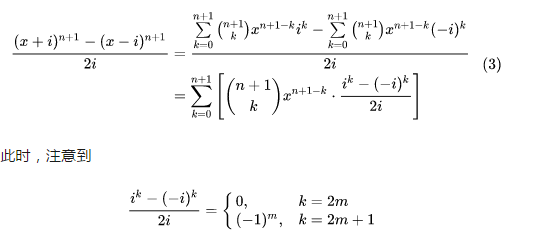 3/4
3/4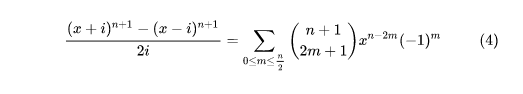 4/4
4/4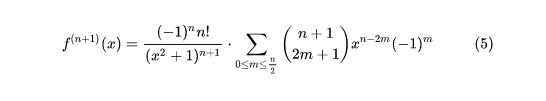
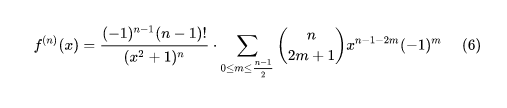 总结1/3
总结1/3
第一步首先我们,设f(x)=arctan x,今将给出f(n)(x)的一种求法。如图1所示。下一步其中,我们权且引入虚数 i 以便将有理分式进行分拆。接下来就将有如图2所示。
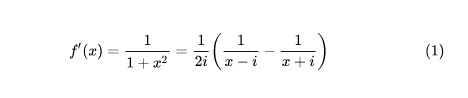
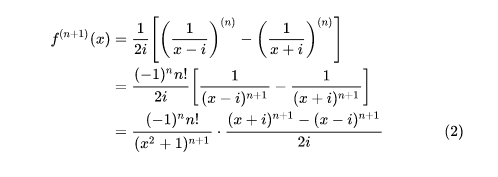 2/4
2/4下一步 这个式子中仍含有 i 直接这样保留着是不行的,需要设法消去。考虑利用Newton二项式定理,如图所示。
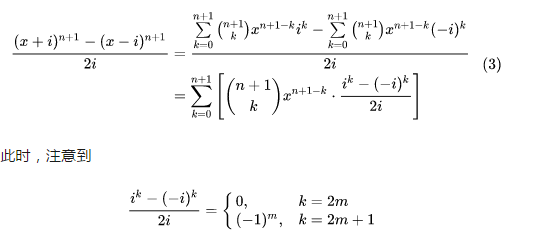 3/4
3/4下一步 这表明上一步(3)之末式求和号下仅剩 k 取小于 n 的正奇数时的诸项,该事实可以记作,如图所示。
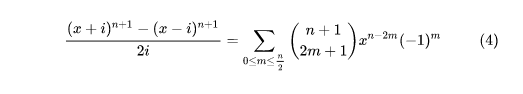 4/4
4/4下一步于是得出,图1。最后一步容易验证上一步(5)对 n=0 也成立,于是将 n—1 作为 n 代入,即得 图2所示。
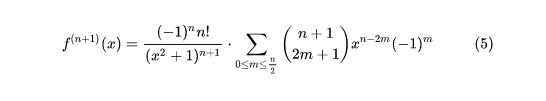
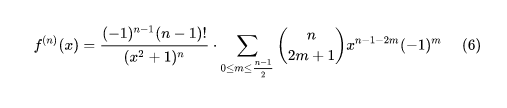 总结1/3
总结1/3设f(x)=arctan x,今将给出f(n)(x)的一种求法。其中,我们权且引入虚数 i 以便将有理分式进行分拆。接下来就将有。
2/3这个式子中仍含有 i 直接这样保留着是不行的,需要设法消去。考虑利用Newton二项式定理。
3/3表明上一步(3)之末式求和号下仅剩 k 取小于 n 的正奇数时的诸项,该事实可以记作,得出后,容易验证上一步(5)对 n=0 也成立,于是将 n—1 作为 n 代入,即得
注意事项公式较多,看清楚在操作
这个公式f(n)(x),(n)在 f 的右上角
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_1126455.html
上一篇:能补充雌性激素的食物有哪些
下一篇:如何在短信中添加图片
 订阅
订阅