教研员用几何画板解圆上动点到直线距离最值题
来源:网络收集 点击: 时间:2024-08-20【导读】:
圆上动点到直线距离最值题是高考的高频题,考查了转化化归与数形结合的思想,在教学法中如何直观进行教学,让学生期待数学,学会用思想的眼光观察世界,用数学的思维分析世界,用数学的语言表达世界,很有帮助,在具体的教学中,我们用几何画板解圆上动点到直线距离最值题,很直观,很方便,还可以当场验证。现将经验介绍如下。工具/原料more几何画板圆上动点到直线距离最值题一条方法/步骤1/7分步阅读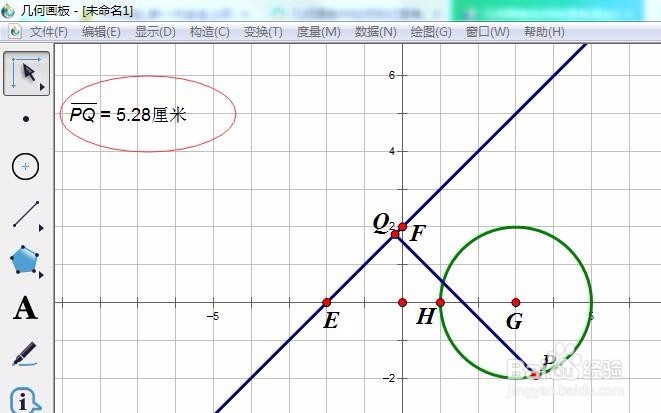 2/7
2/7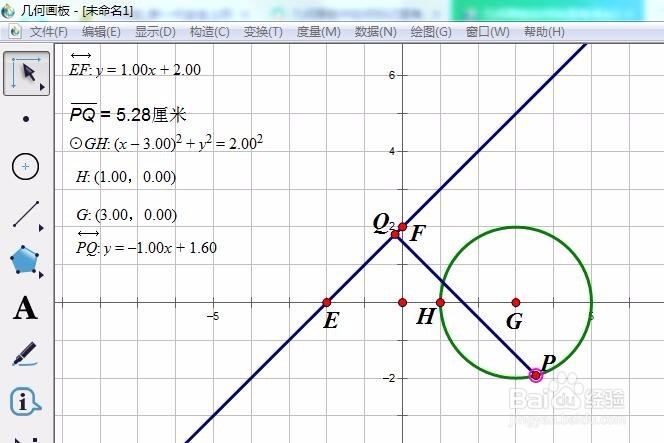 3/7
3/7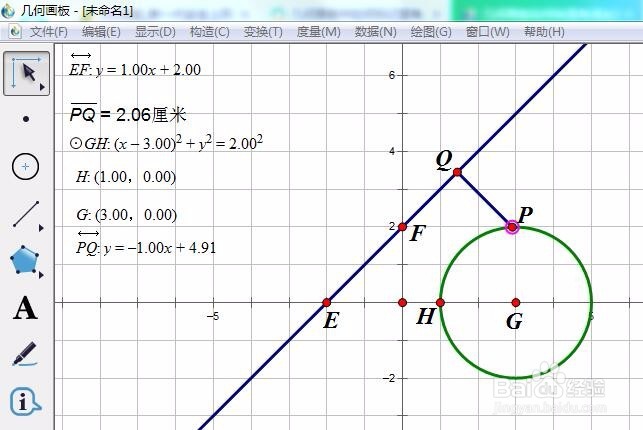 4/7
4/7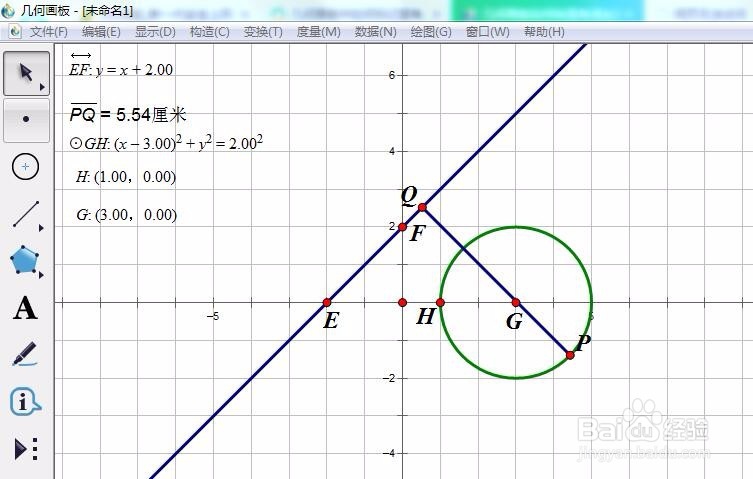 5/7
5/7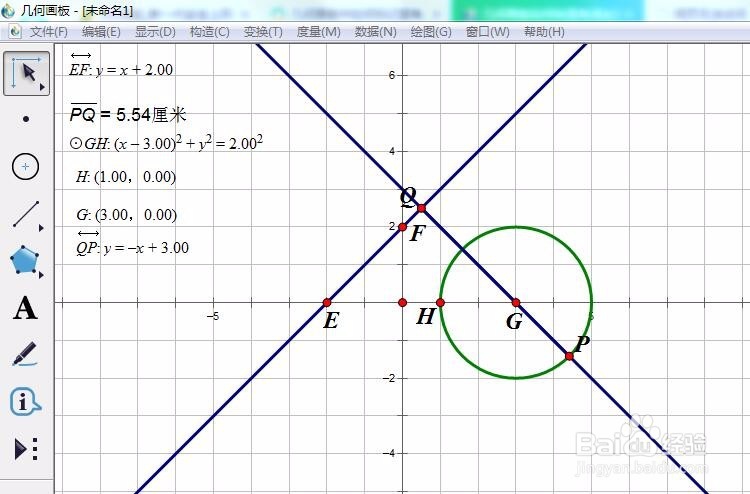 6/7
6/7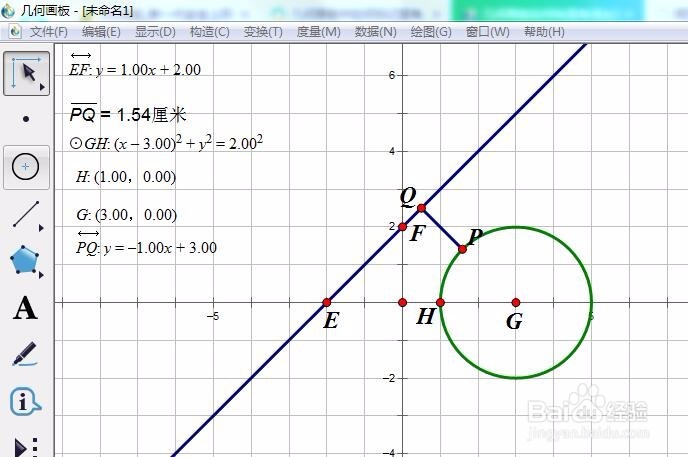 7/7
7/7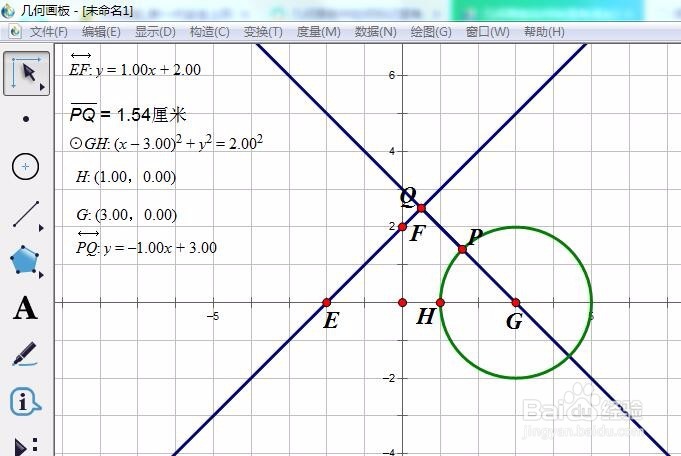 注意事项
注意事项
作出圆(x-3)^2+y^2=2^2
作出直线y=x+2
上作圆上一动点P到直线的垂线段PQ。
 2/7
2/7测量PQ的长度,
如下图,5,28
 3/7
3/7拉动P点在圆上运动。
Q点相应移动,
我们观察PQ长度变大,变小。
 4/7
4/7如下图,我们观察到P点在下图的状态时,
PQ=5.54 为最大值。
此时,PQ过圆心,且圆心是线段PQ的内分点。
我们得到猜想
PQ过圆心,且圆心是线段PQ的内分点时,PQ=5.54 为最大值。
 5/7
5/7验证猜想:
过圆心G作直线y=x+2的垂线,度量该直线的方程,得PQ:y=-x+3
正好过P点。所以猜想成立。
 6/7
6/7类似第五步,得到猜想:
Q=1.54 为最大值。
此时,PQ过圆心,且圆心是线段PQ的外分点。
我们得到猜想
PQ过圆心,且圆心是线段PQ的外分点时,PQ=1.54 为最小值。
 7/7
7/7验证猜想:
过圆心G作直线y=x+2的垂线,度量该直线的方程,得PQ:y=-x+3
正好过P点。所以猜想好成立。
 注意事项
注意事项关于高考数学解题,如果你有什么疑问,欢迎询问。有问必答哦。
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_1143584.html
上一篇:拼多多怎么删除已收藏的商品
下一篇:PPT如何更改渐变背景的颜色?
 订阅
订阅