二项式常数项怎么求
来源:网络收集 点击: 时间:2024-08-28【导读】:
问题:关于x的二项式(a*x+b)^n的常数项,怎么计算?本文,用Mathematica来计算这个问题,并依次算出各项系数。工具/原料more电脑Mathematica方法/步骤1/7分步阅读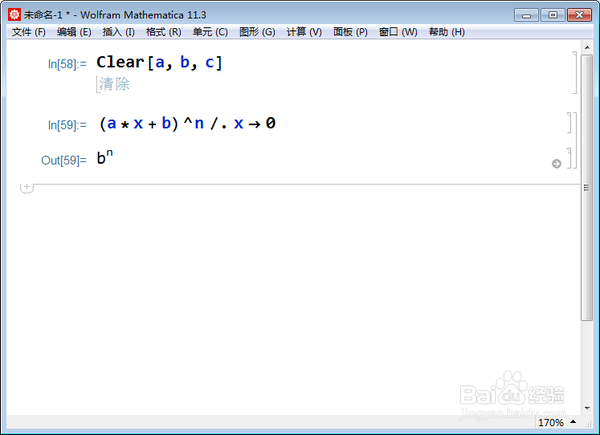 2/7
2/7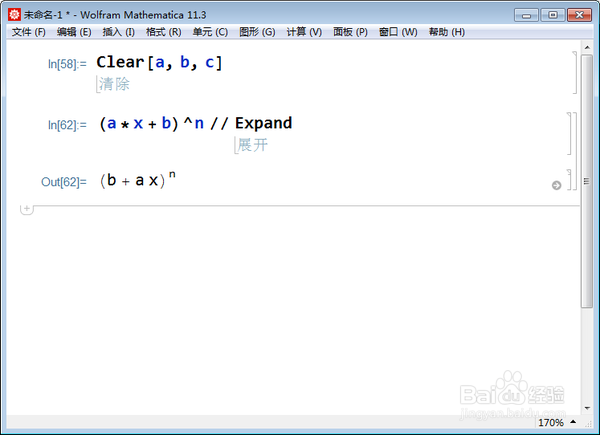 3/7
3/7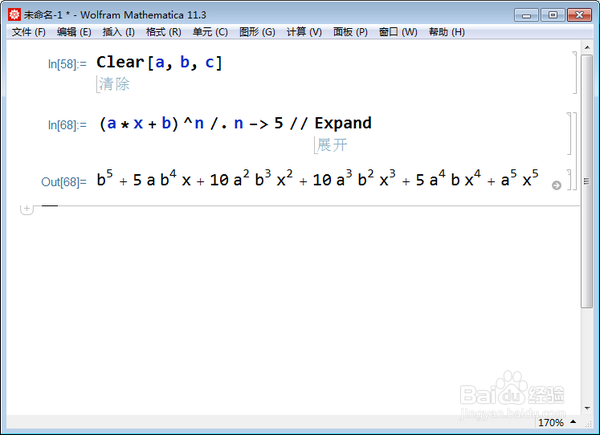 4/7
4/7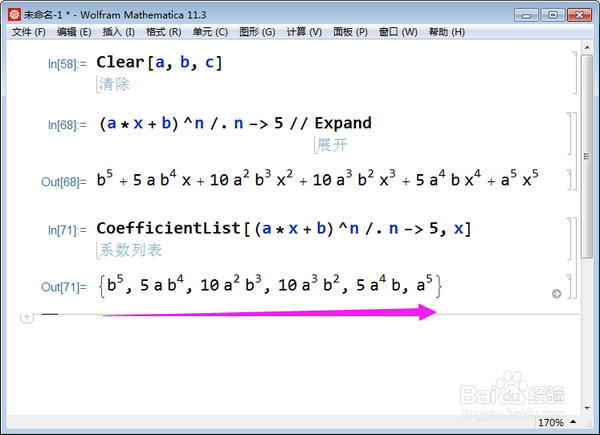 5/7
5/7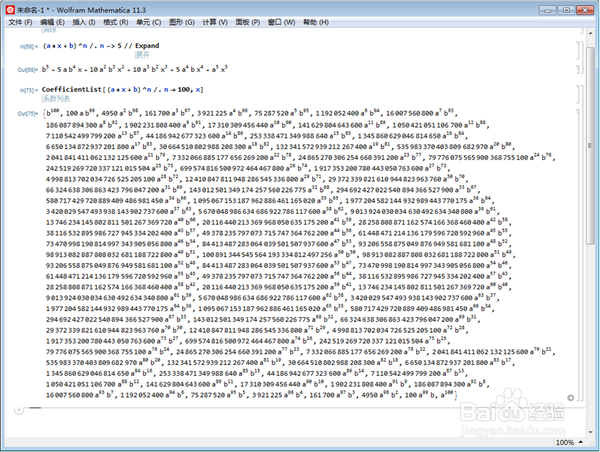 6/7
6/7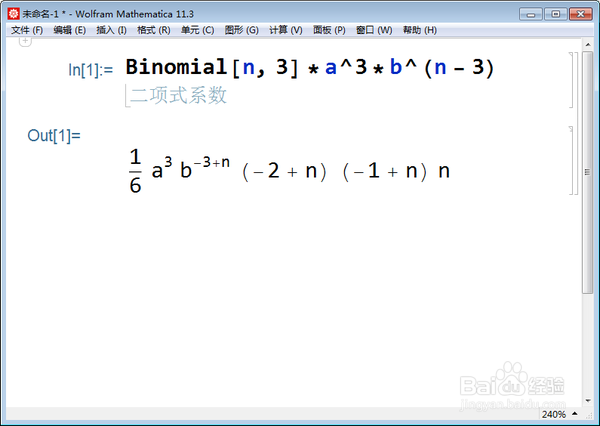 7/7
7/7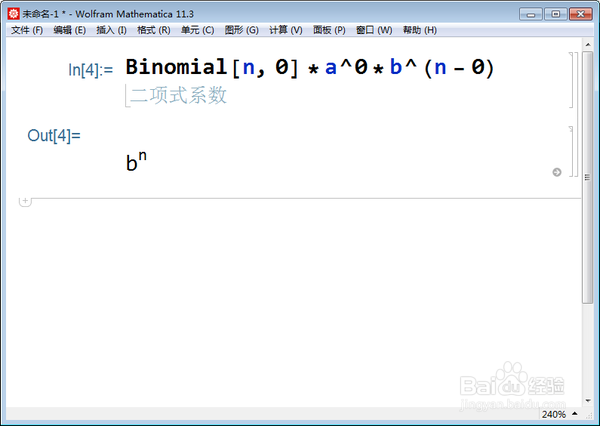
二项式,我们约定n是非负整数,否则就没有常数强拒物项的概念了。
常数项,只需要令x=0,结果就是常数项:
(a*x + b)^n /. x - 0,
答案是b^n。
 2/7
2/7尝试着展开二项式:
(a*x + b)^n // Expand,
没成功,原因很可能是,Mathematica没有把n当成正整数。
 3/7
3/7退而求其次,对n赋予具体的数值,看看能不能展开:
(a*x + b)^n /. n - 5 // Expand,
展开之后,各项系数一目了然。
 4/7
4/7可不可以直接算出各项系数呢?试一试吧。
CoefficientList,
运行结果,系数是从低次项到高次项排列,第一项就是常数项。
 5/7
5/7换一个大一点的指数:
CoefficientList,
项数多,系数长。
 6/7
6/7一个自然的问题是,如果不给n赋值,有没有什么办法,给出二项式各项的系数呢?
比如,计算(a*x+b)^n的三次泥总项系光戴数:
Binomial*a^3*b^(n - 3),
这是直接套用二项式定理的结果。
 7/7
7/7如此一般,可以求出(a*x+b)^n的常数项:
Binomial*a^0*b^(n - 0)。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_1166314.html
上一篇:失信被执行人住星级酒店,酒店会查得出吗
下一篇:QQ怎样在群聊中上传文件
 订阅
订阅