多元函数的极限在高等数学中是非常重要的，但多元函数的自变量太多计算起来太过复杂，而一元函数的极限看起来就相对容易些，因此把多元函数极限转化为一元函数的极限来求解。

例如：

1、lim(x,y)-(0,0) sin(x+y) / (x+y) 令 u = x+y

= lim(u-0) sinu / u = 1

2、f(x,y) = xy / (x+y)

∵ | xy | / (x+y) ≤ (1/2) |x|

lim(x,y)-(0,0) |x| = 0

∴ lim(x,y)-(0,0) xy / (x+y) = 0

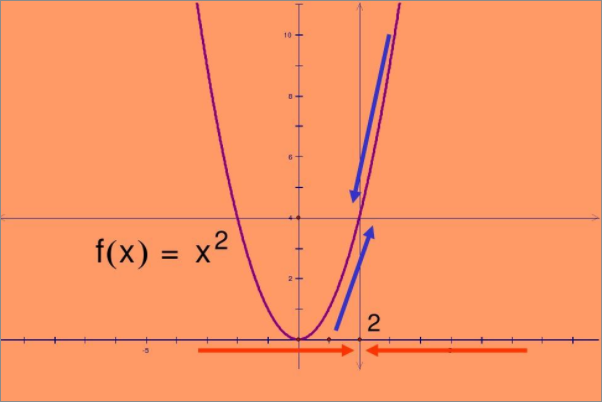
多元函数求极限定理介绍

定理1：设f(x，y，z)在点(x0，y0，z0)的某去心邻域内有定义，cosα，cosβ，cosγ是向量(x-x0，y-y0，z-z0)的方向余弦，若limk0f(x0+kcosα，y0+kcosβ，z0+kcosγ)=A则

(1)当A是与α，β，γ的取值无关的常数时，limxx0yy0zz0f(x，y，z)=A。

(2)当A是与α，β，γ的取值有关的常数时，limxx0yy0zz0f(x，y，z)不存在。

推论(1)设f(x，y，z)在点(0，0，0)的某去心邻域内有定义，cosα，cosβ，cosγ是向量(x，y，z)的方向余弦，若limk0f(kcosα，kcosβ，kcosγ)=A则

(1)当A是与α，β，γ的取值无关的常数时，limxx0yy0zz0f(x，y，z)=A。

(2)当A是与α，β，γ的取值有关的常数时，limxx0yy0zz0f(x，y，z)不存在。

以上内容参考 百度百科—极限