2*2的正定矩阵的判定
来源:网络收集 点击: 时间:2024-02-23【导读】:
用Mathematica来计算,下面的矩阵何时是正定矩阵。给定的矩阵是{{a,b},{c,d}}。工具/原料more电脑Mathematica方法/步骤1/6分步阅读 2/6
2/6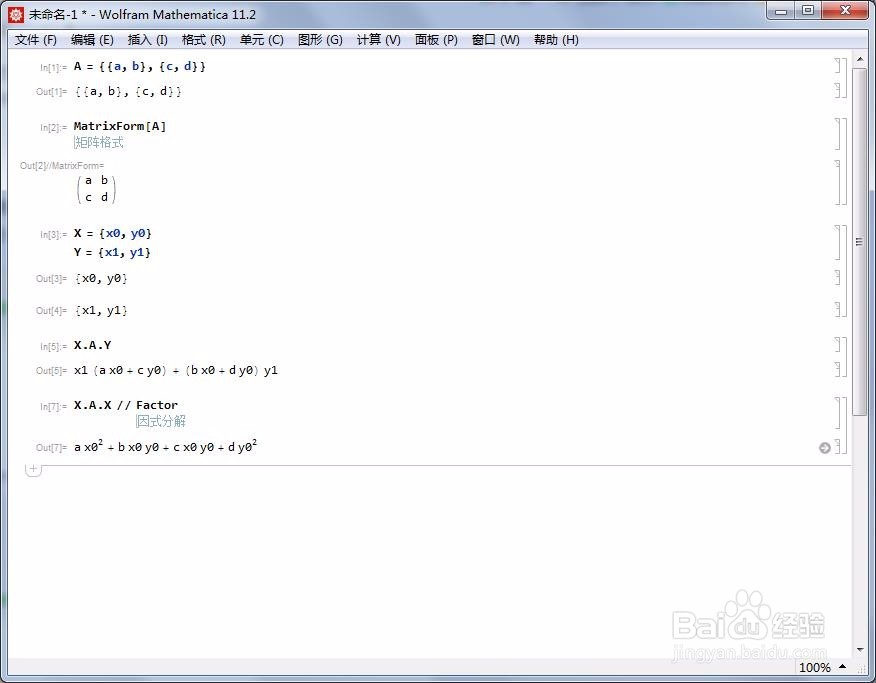 3/6
3/6 4/6
4/6 5/6
5/6
正定矩阵是从双线性型引申出来的。
给定双线性型X,Y=XAY,其中X表示向量X的列向量形式。
如果:
X = {x0, y0}
Y = {x1, y1}
那么,X.A.Y在Mathematica就表示了上面的双线性型,结果等于:
x1 (a x0 + c y0) + (b x0 + d y0) y1
 2/6
2/6而如果A是正定矩阵,那么,对于非零向量X,X,X大于0。
X.A.X // Factor
a x0^2 + b x0 y0 + c x0 y0 + d y0^2
 3/6
3/6用Mathematica求a、b、c、d应该满足的关系:
Reduce != 0]]
 4/6
4/6如果矩阵A是对称矩阵,结果可能会好一点:
A = {{a, b}, {b, d}}
Reduce != 0]]
最后的结论是:
d0且b^2ad。
 5/6
5/6由于这是一个2*2的矩阵,那么,a和d的地位是等同的。
一般的,我满都从左上角开始,依次选取子矩阵,要求各个子矩阵的行列式大于0,所以,第四步的结论可以写为:
a0且b^2ad。
6/6三维情况下,我们仍旧限定A是对称矩阵:
A = {{x, b, c}, {b, y, d}, {c, d, z}}
但是,Mathematica没有给出教材上那么整洁的充要条件。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_124421.html
 订阅
订阅