函数极限计算除了常用的等价无穷小替换、洛必达法则以外，其实最根本最重要的方法是泰勒公式的展开，但泰勒公式是有无穷项的，那么在实际做题中究竟展开到第几项呢？以下就是详细作答。

泰勒公式的核心问题就是究竟展开到哪一项，具体规则如下：

比如这一题，分子就是a-b类型，整体是a/b类型，故根据上述规则，e^x*sinx要展开到x的3次阶。

但是注意，要将e^x*sinx看做一个整体，e^x展开最低次项是1，而sinx展开最低次项是x，故sinx要展开到x的3次方，而e^x只需展开到x的2次方即可，因为即使e^x展开到了x的3次方，哪怕乘上sinx展开的最低次项，结果也是x的4次方也就是高阶无穷小了，故只需将e^x展开到2次方即可。具体展开如图。

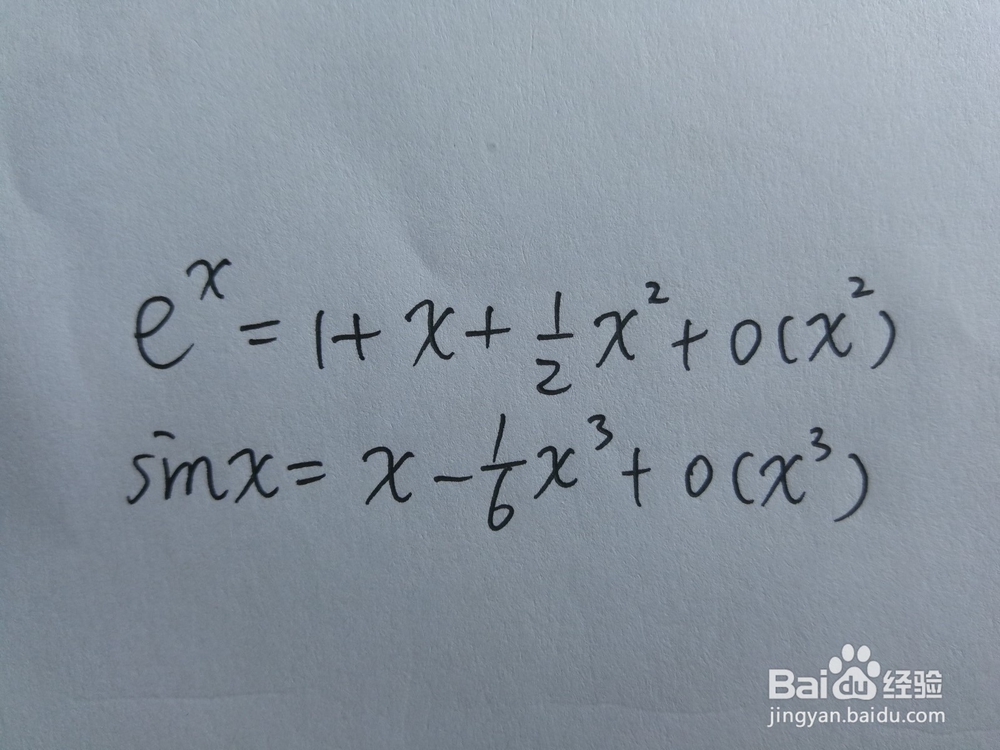
如此一来，上题的具体步骤如图所示。

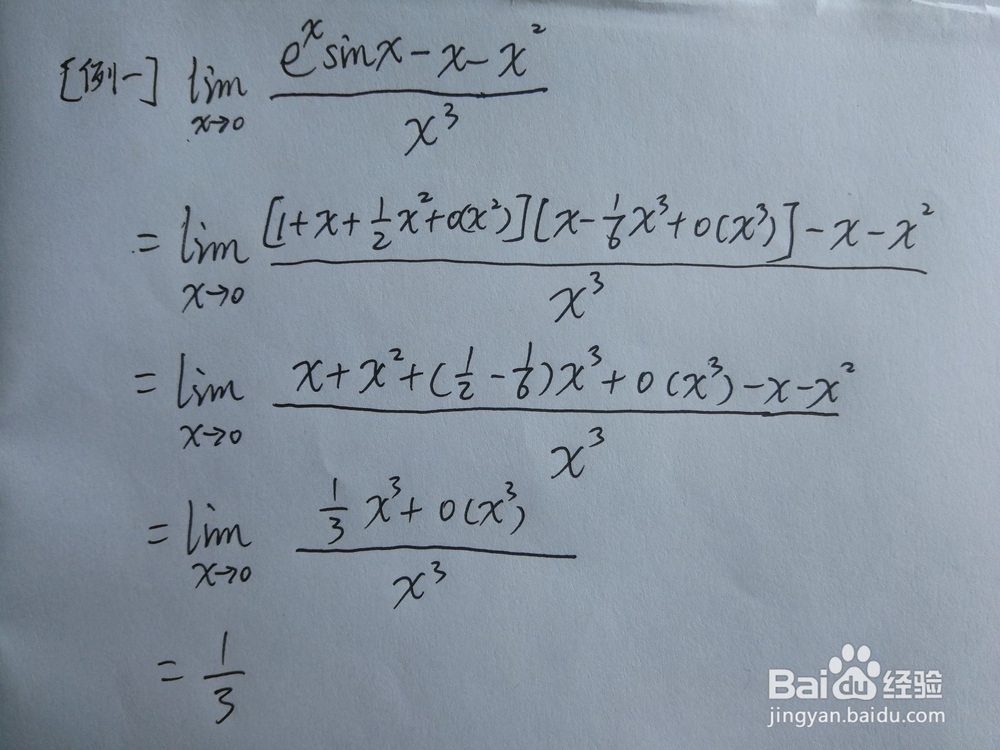
泰勒公式对比洛必达法则，优点在于，它不要求分子分母可导，而且通过展开式能迅速找到两个无穷小之间的差异，但是缺点在于，泰勒公式只能用于未知数趋于0的情况，洛必达可以是趋于无穷大。