订阅【抽象代数】用Mathematica求代数数本原多项式
来源：网络收集 点击： 时间：2024-02-24【导读】：
我们前面介绍了，用Mathematica可以判定代数整数和代数数的方法。那么，给定一个代数数，怎么求它的本原多项式呢？本文，我就来介绍相关命令。工具/原料more电脑Mathematica方法/步骤1/6分步阅读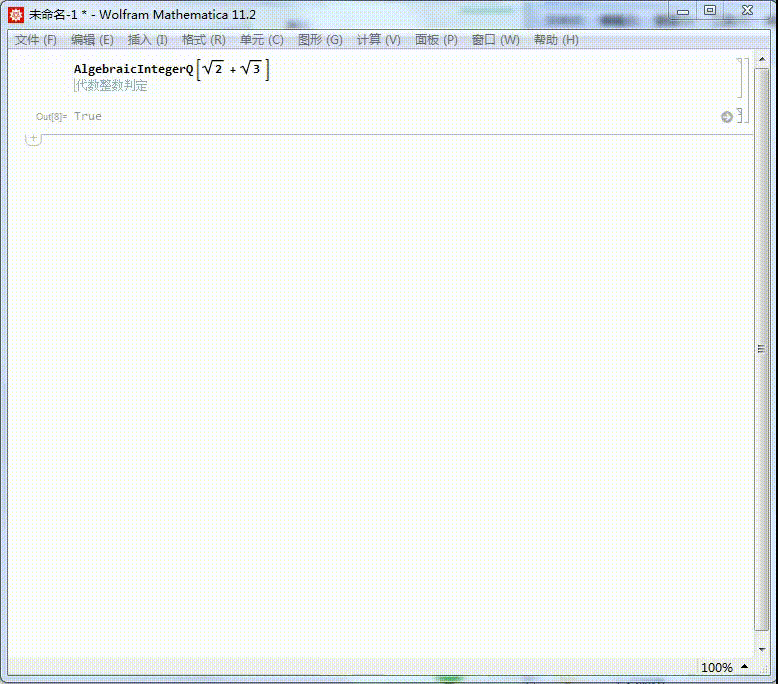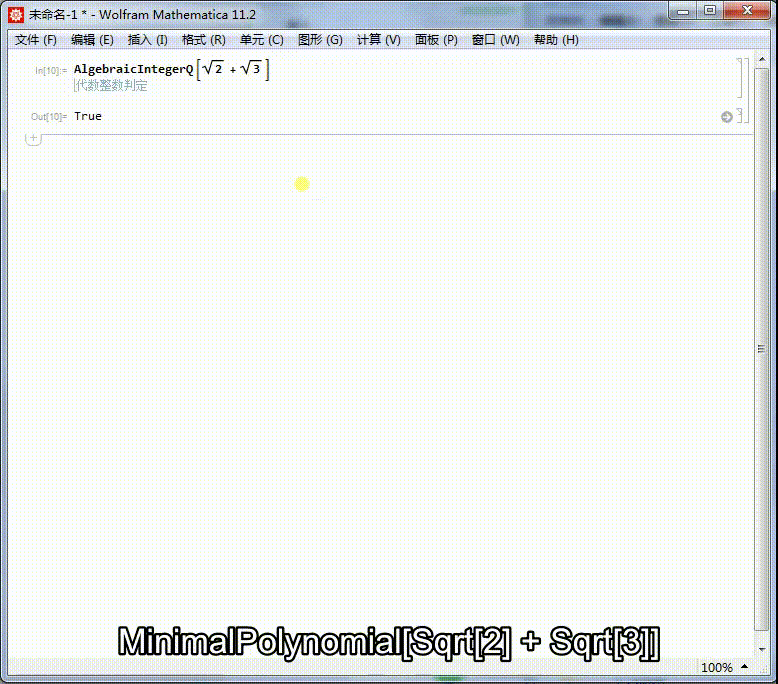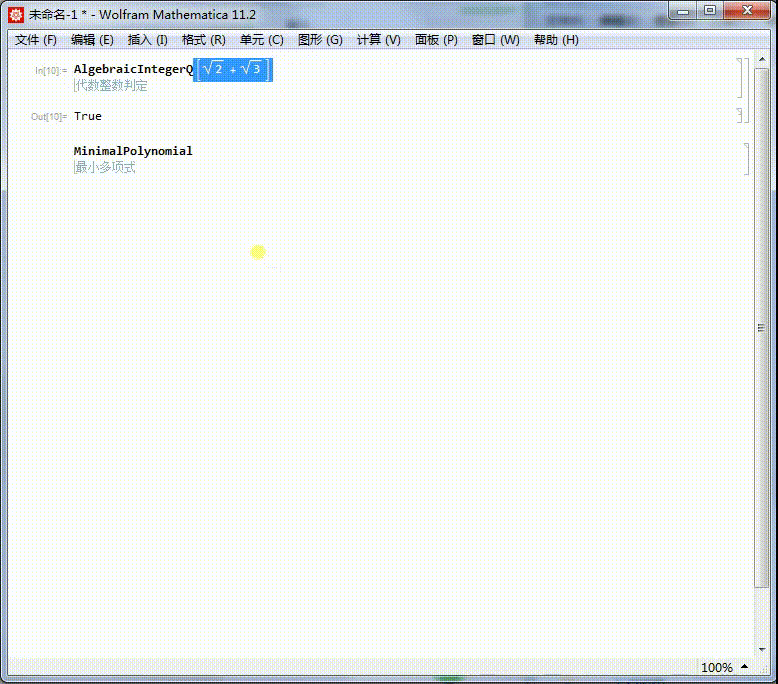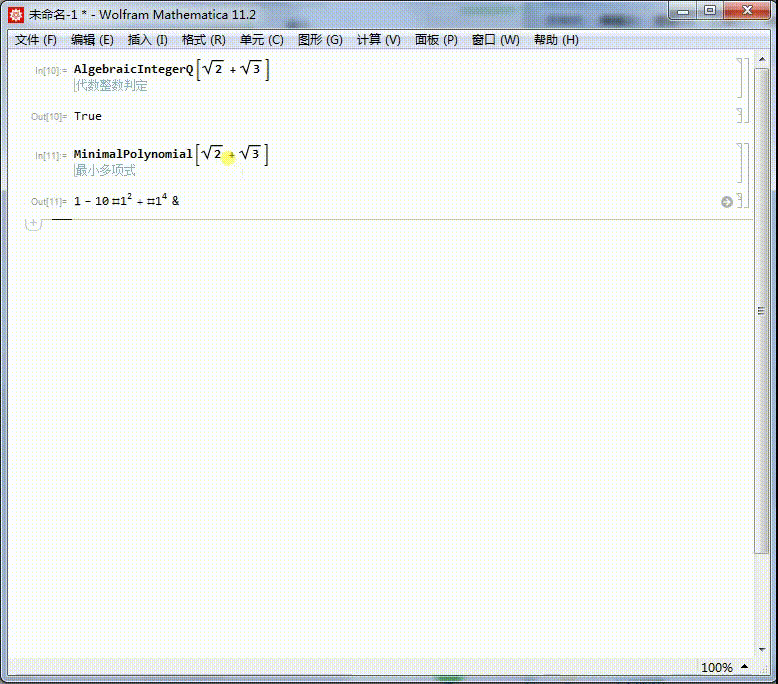
2/6
3/6
4/6
5/6
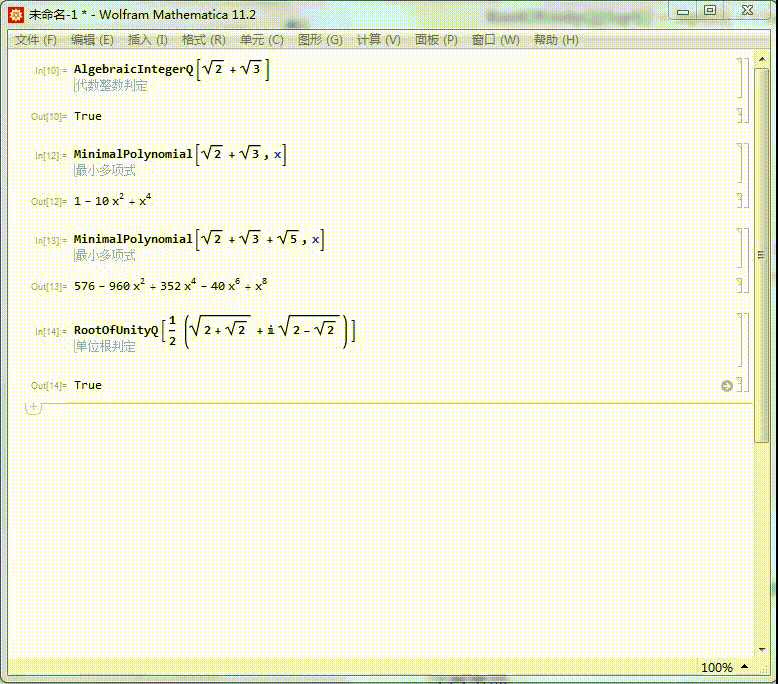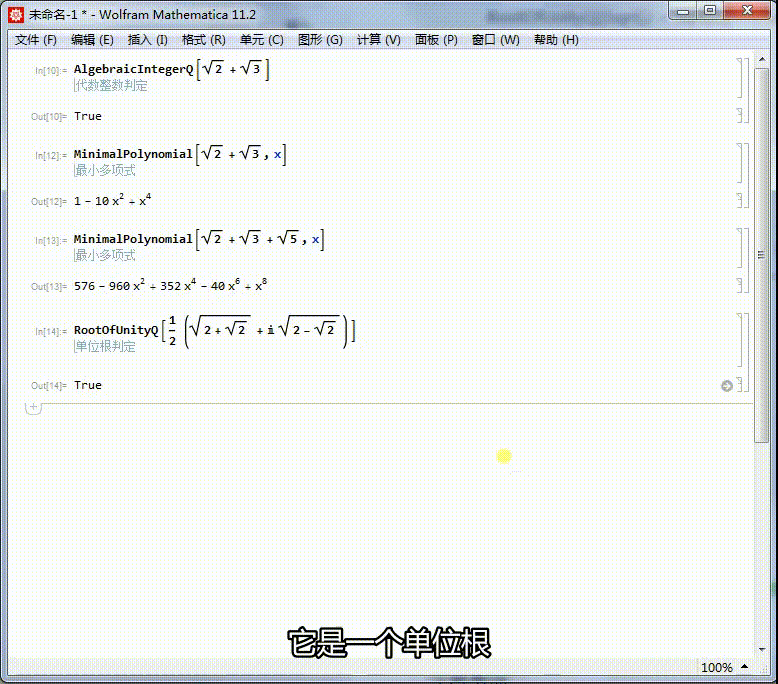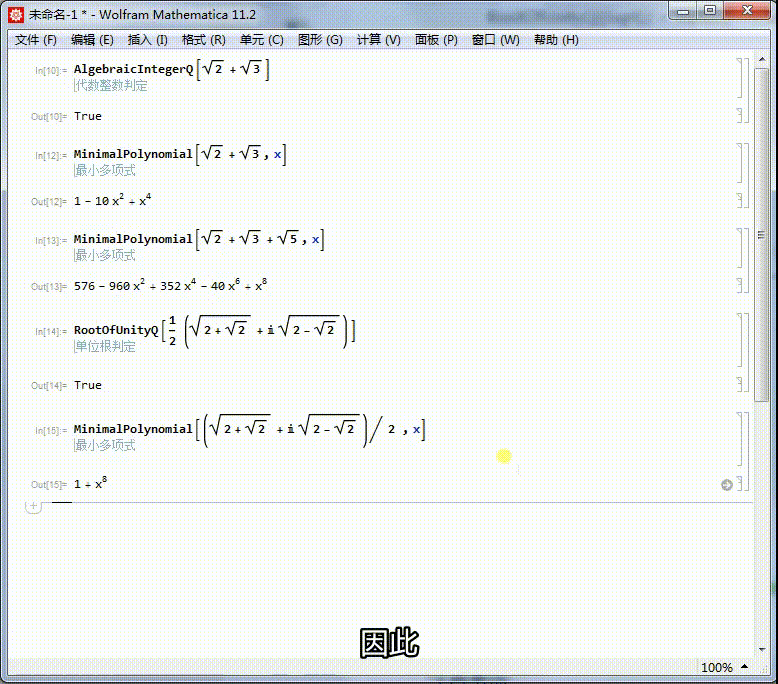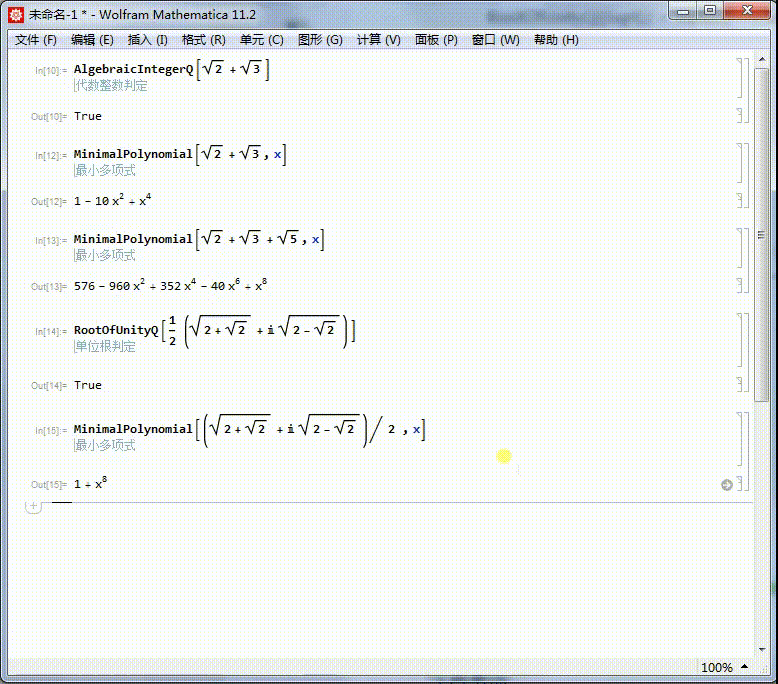6/6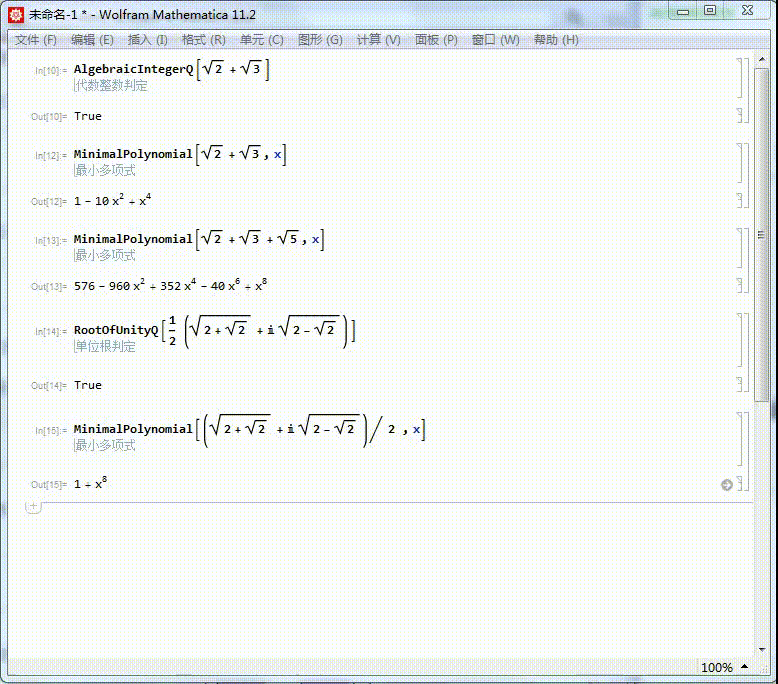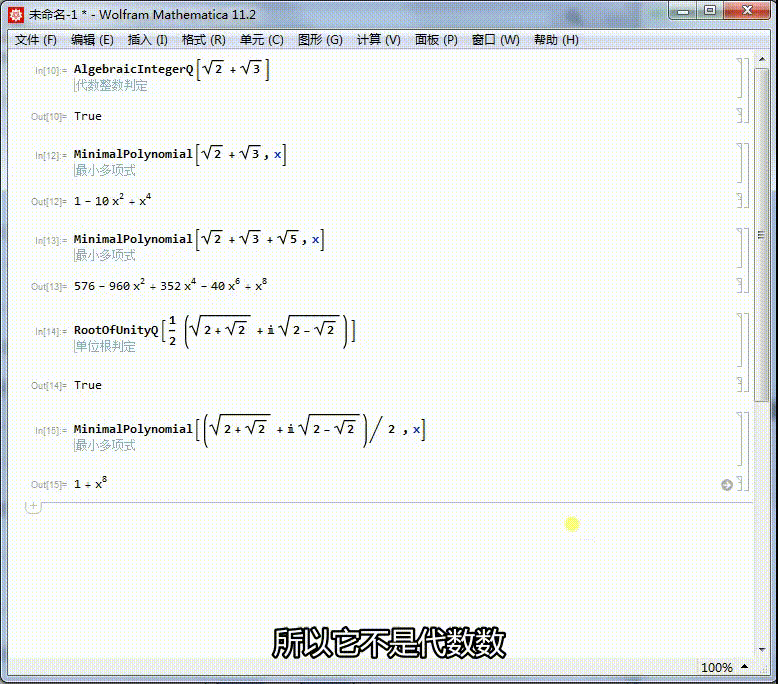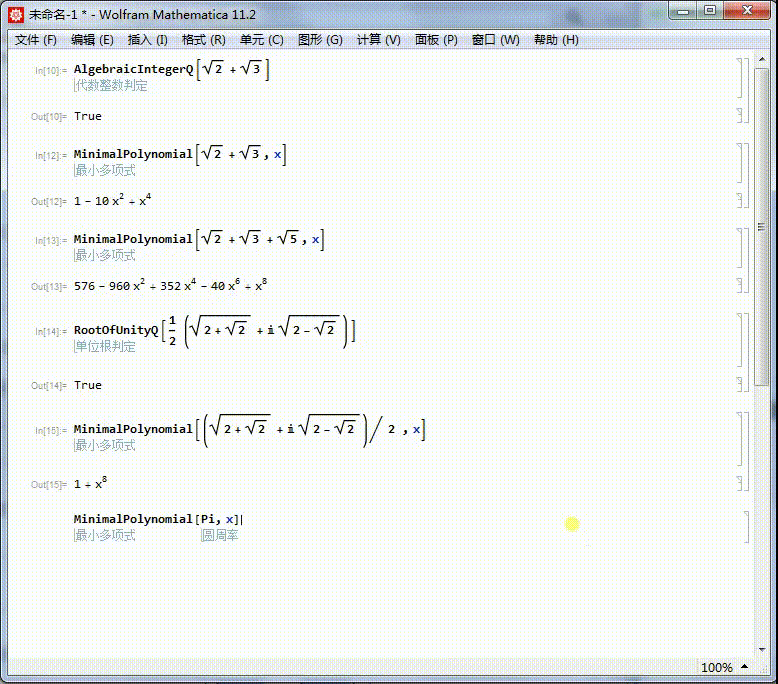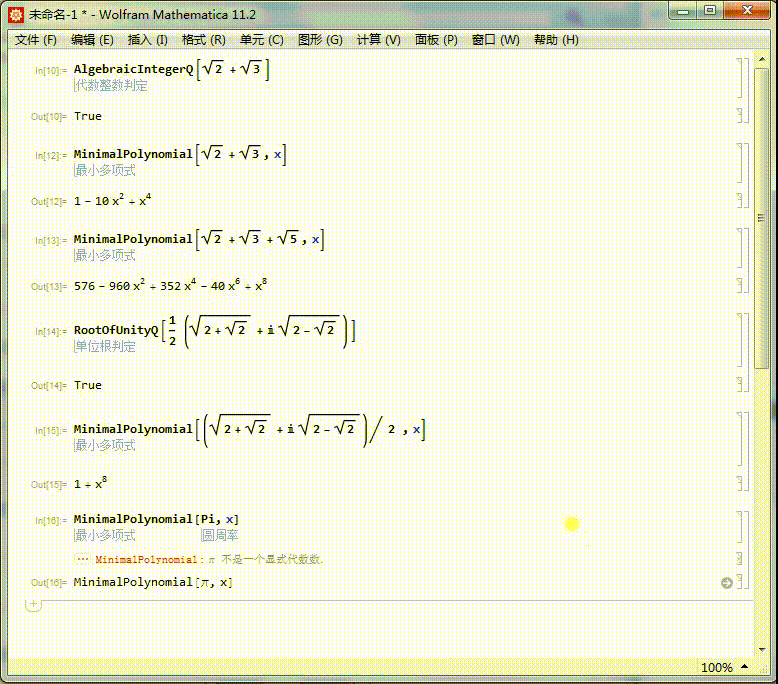
我们知道Sqrt + Sqrt 是代数整数，它的本原多项式是：
MinimalPolynomial + Sqrt]
2/6上面返回的是一个纯函数。如果需要一个关于x的多项式，可以写为：
MinimalPolynomial + Sqrt,x]
3/6同样的，Sqrt + Sqrt + Sqrt的本原多项式也可以求出来，结果得到的多项式有点复杂：
MinimalPolynomial + Sqrt + Sqrt,x]
4/6(Sqrt]+I Sqrt])/2是一个单位根：
RootOfUnityQ] + I Sqrt])/2]
5/6求出它的本原多项式，可以进一步证明，它是一个单位根。
它的本原方程是x^8+1=0，因此，它是一个16次单位根。
6/6圆周率不存在本原多项式，所以它不是代数数。
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_129669.html
上一篇：手机直播伴侣详细教程
下一篇：支付宝如何领取公交卡
