绪：图像主要是基于矩阵格式排列的，因此OpenCV中矩阵操作非常重要；本文总结了：矩阵的创建；矩阵初始化；矩阵运算；矩阵乘法；矩阵转置；矩阵的逆；等操作；方法/步骤1/11分步阅读

OpenCV矩阵的创建：

创建矩阵需要知道矩阵的尺寸大小和数据类型；

矩阵尺寸大小：就是m行n列；Size(5,5);

矩阵数据类型：深度8/32位，类型uchar/float，通道数1/3/4；

CV_8UC1// 8位无符号单通道

CV_8UC3// 8位无符号3通道

CV_8UC4// 8位无符号4通道

CV_32FC1// 32位浮点型单通道

CV_32FC3// 32位浮点型3通道

CV_32FC4// 32位浮点型4通道

一般，采用Mat类创建矩阵：

void main()

{

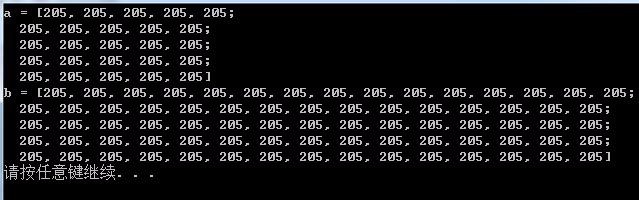
Mat a(Size(5,5),CV_8UC1);//单通道

couta = aendl;

Mat b = Mat(Size(5,5),CV_8UC3);//3通道

coutb = bendl;

system(pause);

}

【注】：3通道矩阵中，一个矩阵元素包含3个变量；

【注】：Mat创建矩阵，默认通过随机值初始化矩阵数值；

2/11

矩阵初始化：

Mat类几种初始化创建方法:

void main()

{

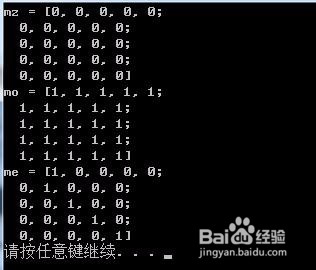
Mat mz = Mat::zeros(Size(5,5),CV_8UC1);//全0矩阵

Mat mo = Mat::ones(Size(5,5),CV_8UC1);//全1矩阵

Mat me = Mat::eye(Size(5,5),CV_32FC1);//对角线为1的对角矩阵

coutmz = mzendl;

coutmo = moendl;

coutme = meendl;

system(pause);

}

3/11

OpenCV矩阵运算：Mat类支持所有矩阵运算；

①使用”+”,”-”符进行矩阵加减运算：

void main()

{

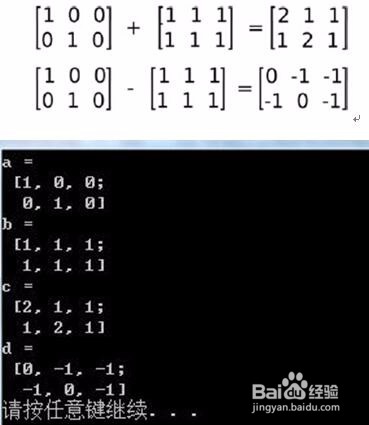
Mat a = Mat::eye(Size(3,2),CV_32FC1);

Mat b = Mat::ones(Size(3,2),CV_32FC1);

Mat c = a+b;

Mat d = a-b;

couta = \n aendl;

coutb = \n bendl;

coutc = \n cendl;

coutd = \n dendl;

system(pause);

}

4/11

矩阵乘法：“*”，“.*”

①使用“*”表示矩阵与标量相乘；

②矩阵与矩阵相乘“*”：满足矩阵相乘条件；

③矩阵和矩阵点乘“.mul()”，对应元素相乘；

void main()

{

Mat m1 = Mat::eye(2,3,CV_32FC1);

Mat m2 = Mat::ones(3,2,CV_32FC1);

coutm1 = \n m1endl;

coutm2 = \n m2endl;

coutm1*2 = \n m1*2endl;//矩阵*标量

cout(m1+2).*(m1+3) = \n (m1+2).mul(m1+3)endl;//矩阵点乘

coutm1*m2 = \n m1*m2endl;//矩阵相乘

system(pause);

}

5/11

矩阵转置：矩阵的行与列对调；

由Mat类t()函数实现：

void main()

{

Mat m1 = Mat::eye(4,6,CV_32FC1);

coutm1 = \n m1endl;

Mat m1t = m1.t();

coutm1t = \n m1tendl;

system(pause);

}

6/11

矩阵的逆：

有两种方法：

①伴随阵法：inv(A)=(1/|A|)×A* ;

其中inv(A)表示矩阵A的逆矩阵，|A|为矩阵A的行列式的值，A*为矩阵A的伴随矩阵。

②行初等变换法：(A|E)经过初等变换得到(E|A^(-1))；

【注】：初等变化只用行(列)运算，不能用列(行)运算,E为单位矩阵;

Mat矩阵的逆由inv()函数实现：

void main()

{

Mat m1 = Mat::eye(5,5,CV_32FC1);

coutm1 = \n m1endl;

Mat m1inv = m1.inv();

coutm1inv = \n m1invendl;

system(pause);

}

7/11

矩阵中非零元素个数：

计算物体的像素或面积常需要用到计算矩阵中的非零元素个数；

OpenCV中使用countNonZero()函数实现。

void main()

{

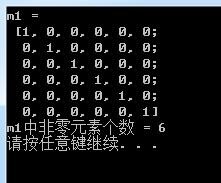
Mat m1 = Mat::eye(6,6,CV_32FC1);

coutm1 = \n m1endl;

int m1num = countNonZero(m1);

coutm1中非零元素个数 = m1numendl;

system(pause);

}

8/11

均值和标准差：

OpenCV提供了矩阵均值和标准差计算功能，

使用meanStdDev(src,mean,stddev)函数实现；

src – 输入矩阵或图像

mean – 均值，OutputArray

stddev – 标准差，OutputArray

void main()

{

Mat m1 = Mat::eye(5,5,CV_32FC1);

coutm1 = \n m1endl;

Mat mean,stddev;

meanStdDev(m1,mean,stddev);

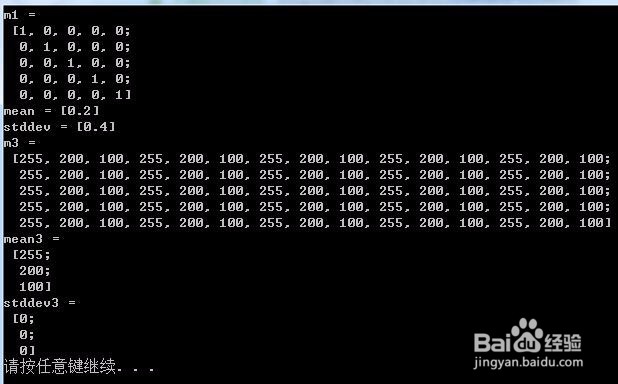
coutmean = meanendl;

coutstddev = stddevendl;

Mat m3(Size(5,5),CV_8UC3,Scalar(255,200,100));

coutm3 = \n m3endl;

Mat mean3,stddev3;

meanStdDev(m3,mean3,stddev3);

coutmean3 = \n mean3endl;

coutstddev3 = \n stddev3endl;

system(pause);

}

【注】：当src为多通道或多维矩阵时，则函数分别计算不同通道的均值与标准差，因此返回的mean和stddev为对应维度的向量；

9/11

求矩阵中元素的最大值最小值：

求输入矩阵的全局最大最小值及其位置，可使用函数：

void minMaxLoc( InputArray src,

CV_OUT double* minVal,

CV_OUT double* maxVal=0,

CV_OUT Point* minLoc=0,

CV_OUT Point* maxLoc=0,

InputArray mask=noArray());

参数：

src – 输入单通道矩阵（图像）.

minVal – 指向最小值的指针， 如果未指定则使用NULL

maxVal – 指向最大值的指针， 如果未指定则使用NULL

minLoc – 指向最小值位置（2维情况）的指针， 如果未指定则使用NULL

maxLoc – 指向最大值位置（2维情况）的指针， 如果未指定则使用NULL

mask – 可选的蒙版，用于选择待处理子区域

int main()

{

Mat img = imread(raw.jpg,0);

imshow(raw_img,img);

double minVal = 0, maxVal = 0;

Point minPt,maxPt;

minMaxLoc(img,minVal,maxVal,minPt,maxPt);

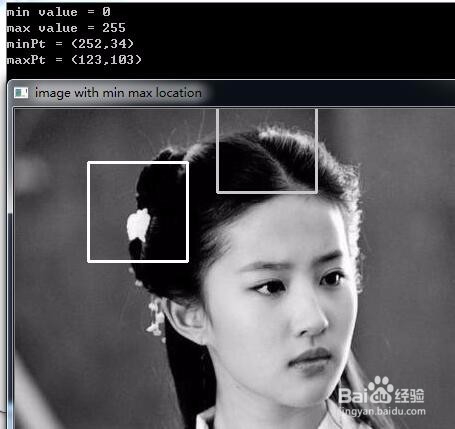
coutmin value = minValendl;

coutmax value = maxValendl;

coutminPt = (minPt.x,minPt.y)endl;

coutmaxPt = (maxPt.x,maxPt.y)endl;

Rect rectMin(minPt.x-50,minPt.y-50,100,100);

Rect rectMax(maxPt.x-50,maxPt.y-50,100,100);

rectangle(img,rectMin,Scalar(200),2);

rectangle(img,rectMax,Scalar(255),2);

imshow(image with min max location,img);

waitKey(0);

return 0;

}

10/11

计算矩阵的特征值和特征向量；

正定矩阵(positive definite matrix):矩阵的特征值都是正数;

半正定矩阵(semi-definite matrix):矩阵的特征值都是非负数(正数和0);

判断矩阵是否正定或者半正定就需要计算矩阵的特征值和特征向量,

使用OpenCV中的eigen()函数进行计算；

#include opencv2\opencv.hpp

using namespace std;

using namespace cv;

int main()

{

double myArray =

{

2, 1, 0,

1, 3, 1,

0, 1, 2

};

Mat myMat = Mat(3, 3, CV_64FC1, myArray);//创建矩阵

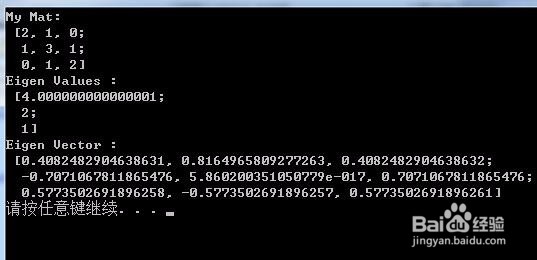
cout My Mat: \n myMatendl;

Mat eValuesMat;//特征值

Mat eVectorsMat;//特征向量

eigen(myMat, eValuesMat, eVectorsMat);

cout Eigen Values : \n eValuesMatendl;

cout Eigen Vector : \n eVectorsMatendl;

system(pause);

return 0;

}

11/11

其他矩阵运算：

Function (函数名) Use (函数用处)

add：矩阵加法，A+B的更高级形式，支持mask；

scaleAdd：矩阵加法，缩放因子dst(I) = scale * src1(I) + src2(I)；

addWeighted：矩阵加法，缩放因子dst(I) = saturate(src1(I) * alpha + src2(I) * beta + gamma)；

subtract：矩阵减法，A-B的更高级形式，支持mask；

multiply：矩阵逐元素乘法，同Mat::mul()函数，与A*B区别，支持mask；

gemm：一个广义的矩阵乘法操作；

divide：矩阵逐元素除法，与A/B区别，支持mask；

abs：对每个元素求绝对值；

absdiff：两个矩阵的差的绝对值；

exp求每个矩阵元素 src(I) 的自然数 e 的 src(I) 次幂 dst = esrc(I)；

pow求每个矩阵元素 src(I) 的 p 次幂 dst = src(I)p；

log求每个矩阵元素的自然数底 dst = log|src(I)| (if src != 0)；

sqrt求每个矩阵元素的平方根；

min, max求每个元素的最小值或最大值返回这个矩阵 dst(I) = min(src1(I), src2(I)), max同minMaxLoc定位矩阵中最小值、最大值的位置；

compare返回逐个元素比较结果的矩阵；

bitwise_and, bitwise_not, bitwise_or, bitwise_xor每个元素进行位运算，分别是和、非、或、异或；

cvarrToMat旧版数据CvMat,IplImage,CvMatND转换到新版数据Mat；

extractImageCOI从旧版数据中提取指定的通道矩阵给新版数据Mat；

randu以Uniform分布产生随机数填充矩阵，同 RNG::fill(mat, RNG::UNIFORM)；

randn以Normal分布产生随机数填充矩阵，同 RNG::fill(mat, RNG::NORMAL)；

randShuffle随机打乱一个一维向量的元素顺序；

theRNG()返回一个默认构造的RNG类的对象，theRNG()::fill(...)；

reduce矩阵缩成向量；

repeat矩阵拷贝的时候指定按x/y方向重复；

split多通道矩阵分解成多个单通道矩阵；

merge多个单通道矩阵合成一个多通道矩阵；

mixChannels矩阵间通道拷贝，如Rgba到Rgb和Alpha；

sort, sortIdx为矩阵的每行或每列元素排序；

setIdentity设置单元矩阵；

completeSymm矩阵上下三角拷贝；

inRange检查元素的取值范围是否在另两个矩阵的元素取值之间，返回验证矩阵；

checkRange检查矩阵的每个元素的取值是否在最小值与最大值之间，返回验证结果bool；

sum求矩阵的元素和；

mean求均值；

meanStdDev均值和标准差；

countNonZero统计非零值个数；

cartToPolar, polarToCart笛卡尔坐标与极坐标之间的转换；

flip矩阵翻转；

transpose矩阵转置，比较 Mat::t() AT；

trace矩阵的迹；

determinant行列式 |A|, det(A)；

eigen矩阵的特征值和特征向量；

invert矩阵的逆或者伪逆，比较 Mat::inv()；

magnitude向量长度计算 dst(I) = sqrt(x(I)2 + y(I)2)；

Mahalanobis距离计算；

phase相位计算，即两个向量之间的夹角；

norm求范数，1-范数、2-范数、无穷范数；

normalize标准化；

mulTransposed矩阵和它自己的转置相乘 AT * A, dst = scale(src - delta)T(src - delta)；

convertScaleAbs先缩放元素再取绝对值，最后转换格式为8bit型；

calcCovarMatrix计算协方差阵；

solve求解1个或多个线性系统或者求解最小平方问题(least-squares problem)；

solveCubic求解三次方程的根；

solvePoly求解多项式的实根和重根；

dct, idct正、逆离散余弦变换，idct同dct(src, dst, flags | DCT_INVERSE)；

dft, idft正、逆离散傅立叶变换, idft同dft(src, dst, flags | DTF_INVERSE)；

LUT查表变换；

getOptimalDFTSize返回一个优化过的DFT大小；

mulSpecturms两个傅立叶频谱间逐元素的乘法；

注意事项

eigen：矩阵的特征值和特征向量

absdiff：两个矩阵的差的绝对值

minMaxLoc：定位矩阵中最小值、最大值的位置

矩阵OPENCV矩阵图像矩阵矩阵操作矩阵特征值