Mathematica 正态分布与概率计算
来源:网络收集 点击: 时间:2024-02-28【导读】:
介绍Mathematica中概率密度积分,概率分布,表达式的概率计算,概率分布变换。并以正态分布举例说明。工具/原料moreMathematica 11.0方法/步骤1/6分步阅读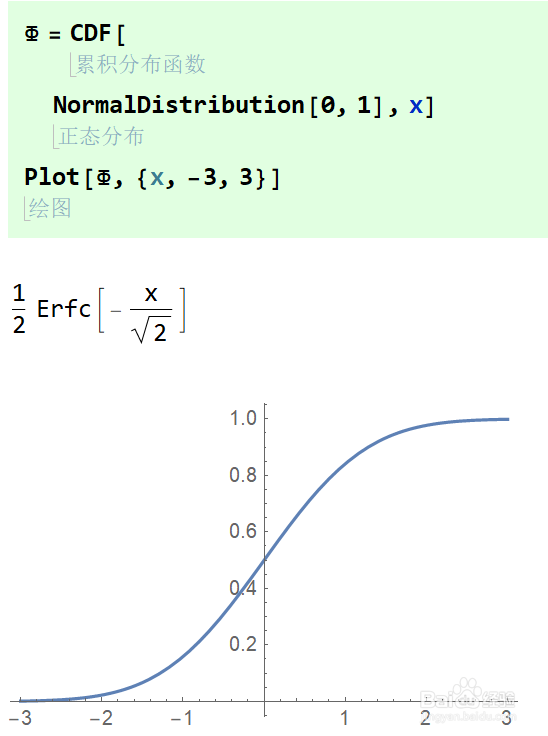 2/6
2/6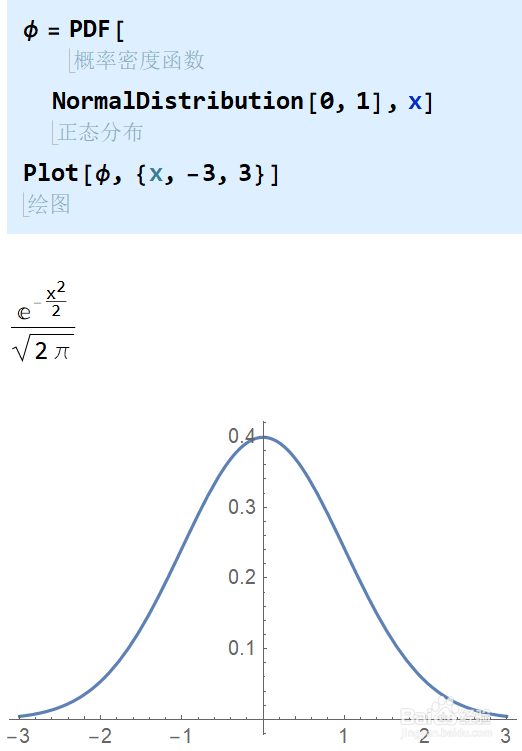 3/6
3/6 4/6
4/6 5/6
5/6 6/6
6/6 注意事项
注意事项
Mathematica中,概率分布符号定义是XXXDistribution.
正态分布为NormalDistribution。分布本身只是分布的符号定义,不是概率密度或者累积分布。要得到累积分布,需要使用CDF函数,如图。
 2/6
2/6类似的,使用函数PDF得到概率密度函数,就是我们熟悉的形式。
而CDF相当于PDF从-∞到x的积分。
 3/6
3/6正态分布NormalDistribution的两个参数含义是,平均值μ和标准差σ。注意是标准差不是方差!
省略参数将表示标准正态分布。
 4/6
4/6要想计算一个区间上的概率,比如-2x2的概率:
第一种方法:可以使用累计分布CDF函数,带入两个边界值相减。做法如图。
 5/6
5/6第二种方法:使用Probability函数。第一个参数为随机变量取值范围表达式,第二个参数为随机变量指示概率分布,如图。
那个双波浪线符号使用 dist 输入。
第三种方法:对概率密度函数积分。如图。
 6/6
6/6如果已知X的分布,求变换a*X+b的分布,使用TransformedDistribution函数。限于篇幅不详细说明该函数。用法如图。
 注意事项
注意事项正态分布是常用分布,Mathematica还有很多分布,可以搜索概率分布或者正态相关分布查看。
符号带入计算的结果可能没有完全化简,需要使用FullSimplify化简。
MATHEMATICA概率密度概率分布正态分布版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_165950.html
上一篇:WPS如何绘制一个正方形
下一篇:进入斗鱼我的推广收益页面
 订阅
订阅