数论:欧拉函数的计算与性质(Mathematica)
来源:网络收集 点击: 时间:2024-03-03【导读】:
使用Mathematica计算欧拉函数,验证有关性质,包括素数的欧拉函数值,欧拉函数的积性性质,欧拉函数的一般计算方法。工具/原料moreMathematica方法/步骤1/7分步阅读 2/7
2/7 3/7
3/7 4/7
4/7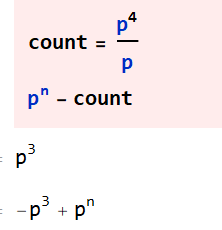 5/7
5/7 6/7
6/7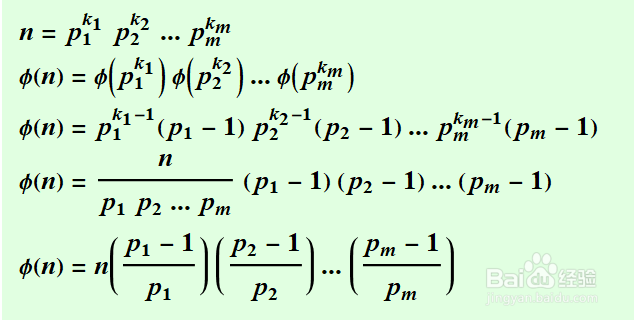 7/7
7/7 注意事项
注意事项
性质1:当p为素数时,p^n的欧拉函数值,等于(p-1)p^(n-1)。
下面,我们举例验证。首先使用Prime函数产生10个素数,依次令n等于2,3,4,5,10计算欧拉函数。
 2/7
2/7产生的10个素数为第一行所示。
下边是对公式的验证,可见数值都是一致的。
 3/7
3/7下边我们举例简要说明原因。
p^n的质因子只有p。故与p^n不互素的只有p的倍数,即0,p,2p,3p...p^n-p。
 4/7
4/7这些不互素的一共有p^n/p个。
用完系中所有元素减去不互素的元素,剩下的元素就是缩系的元素。
元素个数为p^n-p^n/p=(p-1)p^(n-1)
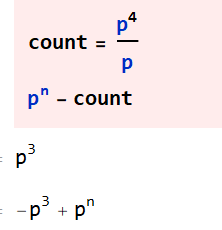 5/7
5/7性质2:欧拉函数的极性。
如图,计算m*n的欧拉函数值,其中m和n互素。
则EulerPhi=EulerPhi*EulerPhi。
如果m和n不互素则不成立。
 6/7
6/7然后是一般情况下,欧拉函数的计算流程。其中用到了前两个性质。
把n质因数分解,然后把各个质因子带入最终公式,计算欧拉函数值。
证明过程如图。
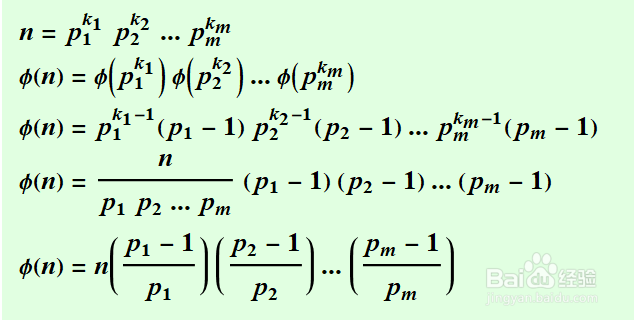 7/7
7/7如图举了一个实际的例子,计算EulerPhi。
把这个数质因子分解,质因子有2,3,41。
把这三个数带入最终公式,算得240。
 注意事项
注意事项关于欧拉函数的含义以及完系和缩系的定义,请查阅经验引用。
理工学科MATHEMATICA欧拉函数数论版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_222731.html
上一篇:wps表格怎么取消限制条件
下一篇:如何为图片添加文本注释?
 订阅
订阅