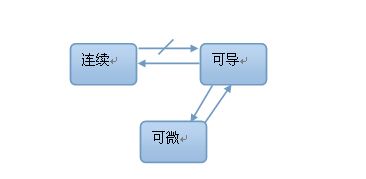
一元函数中可导与可微等价，即为充分必要条件。多元函数可微必可导，而反之不成立，即可导是可微的充分不必要条件。

拓展资料：

微分在数学中的定义：由函数B=f(A)，得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。微积分的基本概念之一。

导数（Derivative）是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f(x0)或df(x0)/dx。

可微和可导对一元单值函数来说是等价的，但是对于一般的函数来说是不等价的。一个这样的多元向量函数在一点可微，当且仅当它的所有偏导数在那一点存在并连续。这是因为导数和微分本质是两种东西，前者是函数在某个方向上的变化率，后者是映射的局部线性近似。