使用MATLAB进行数据分析计算经常需要用到进行多项式求解，和进行曲线拟合一些特性方程曲线，常用方法有最小二乘法和统计回归法。下面分享给大家使用MATLAB进行多项式求解和曲线拟合的方法、程序代码和步骤，希望能够帮助大家。工具/原料more电脑MATLABMATLAB多项式求解和曲线拟合MATLAB多项式求解1/2分步阅读

第一步：我们首先学习MATLAB多项式求解，有两种求解方法，一种是利用polyval 函数求解单个多项式，一种是利用polyvalm 函数求解多个多项式。二者的求解代码如下：

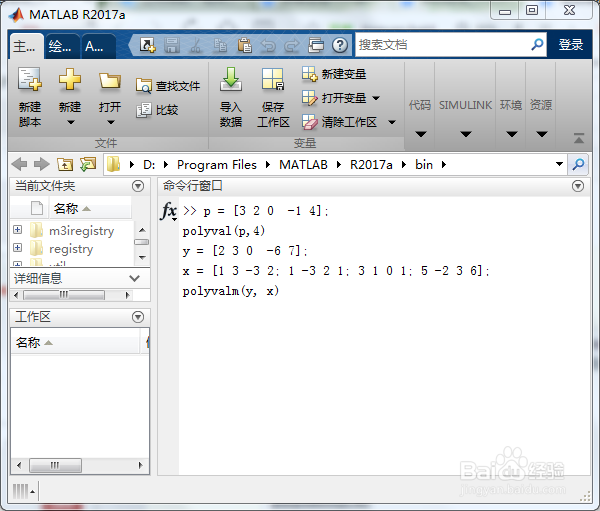
p = ;

polyval(p,4)

y = ;

x = ;

polyvalm(y, x)

我们将其写入到MATLAB程序中，如下图所示。

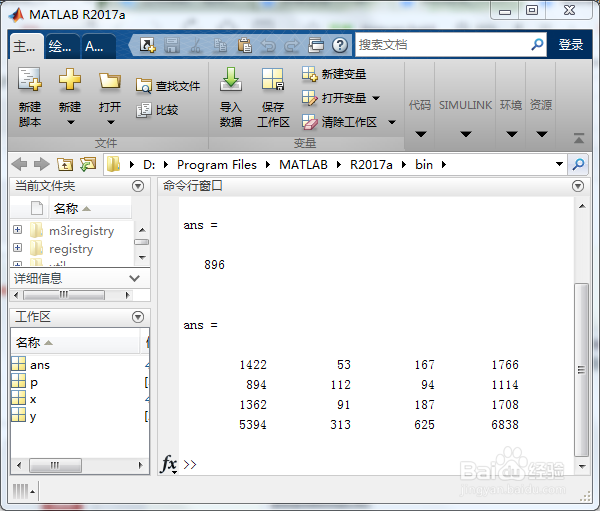
2/2

第二步：我们运行上述MATLAB求解多项式程序代码，得出的运行结果为：

ans =

896

ans =

1422 53 167 1766

894 112 94 1114

1362 91 187 1708

5394 313 625 6838

如下图所示。

MATLAB多项式曲线拟合1/6

第一步：我们对多项式进行曲线拟合可以使用polyfit函数，该函数能够很好地进行曲线拟合，用法MATLAB程序代码为：

p = polyfit(x,y,n)

我们可以输入到MATLAB中按F1查看该函数更多信息。

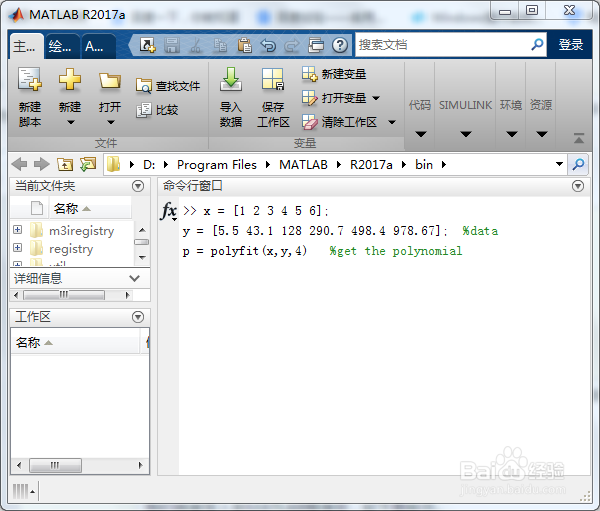
2/6

第二步：知道了曲线拟合polyfit函数的用法后，我们编写程序进行曲线拟合，如果不需要输出图形则使用如下程序代码：

x = ;

y = ; %data

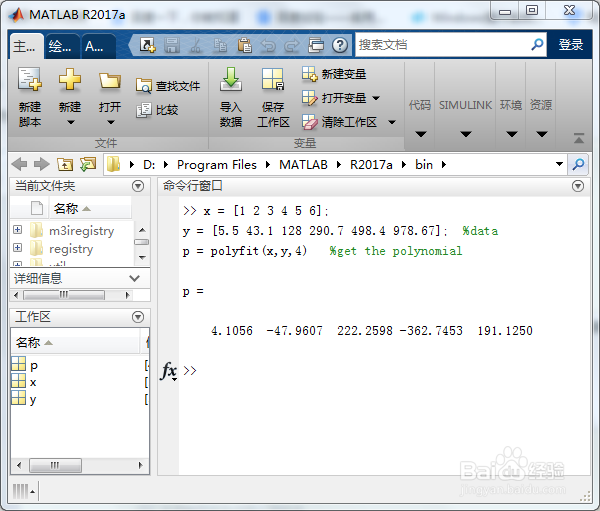
p = polyfit(x,y,4) %get the polynomial

我们将其写入到MATLAB程序中，如下图所示。

3/6

第三步：我们再运行上面的拟合程序代码，可以得出的拟合方程式的系数为：

p =

4.1056 -47.9607 222.2598 -362.7453 191.1250

如下图所示。

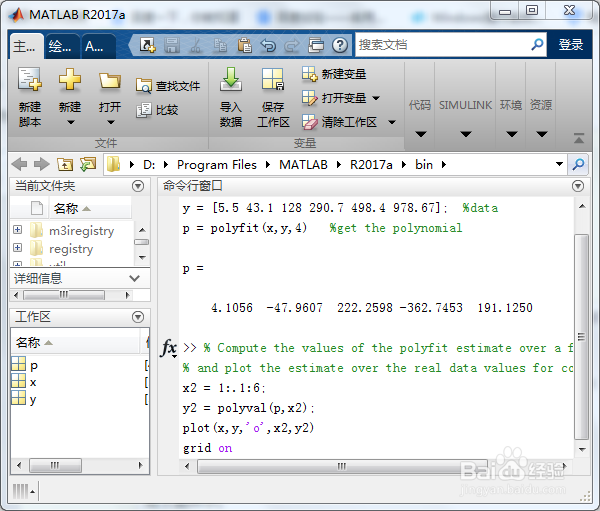
4/6

第四步：如果我们需要直观的显示曲线拟合效果，绘图是少不了了，我们在上述代码的后面加上如下代码：

% Compute the values of the polyfit estimate over a finer range,

% and plot the estimate over the real data values for comparison:

x2 = 1:.1:6;

y2 = polyval(p,x2);

plot(x,y,o,x2,y2)

grid on

如下图所示。

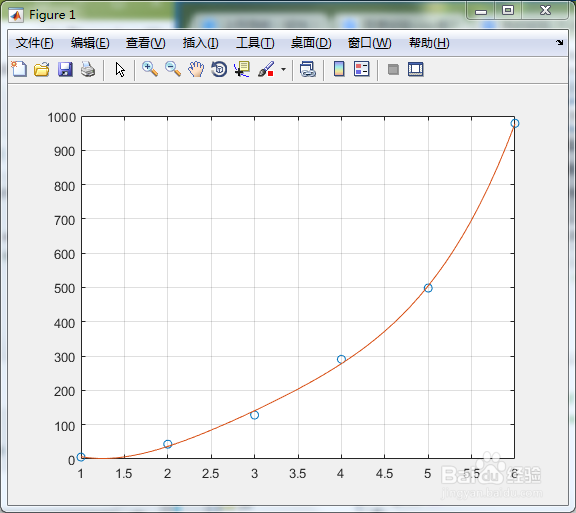
5/6

第五步：我们再次运行程序，可以得出MATLAB多项式曲线拟合的图形如下图所示，我们可以看到该曲线拟合效果是很好的。

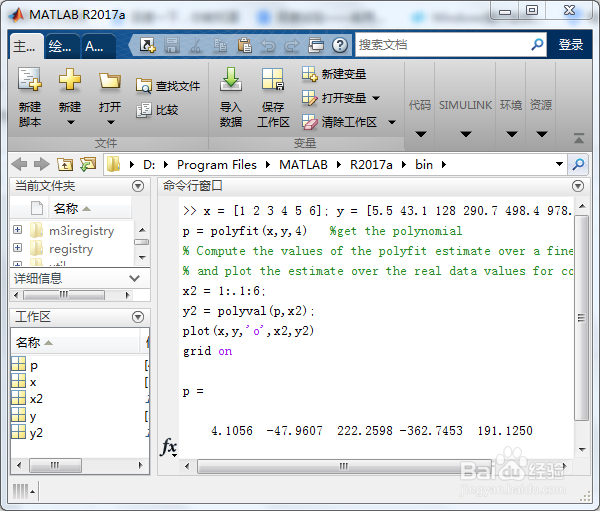
6/6

第六步：完整程序代码如下：

x = ; y = ; %data

p = polyfit(x,y,4) %get the polynomial

% Compute the values of the polyfit estimate over a finer range,

% and plot the estimate over the real data values for comparison:

x2 = 1:.1:6;

y2 = polyval(p,x2);

plot(x,y,o,x2,y2)

grid on

注意事项

上面是使用MATLAB进行多项式求解和曲线拟合的方法、程序代码和步骤，不足之处望以修改指正。

上面是使用polyfit 函数进行多项式曲线拟合，MATLAB还有其他曲线拟合的函数，我们根据实际情况进行选择和使用，方法类似。

MATLABMATLAB多项式MATLAB曲线拟合