参数方程的二阶导数的计算方法
来源:网络收集 点击: 时间:2024-03-08已知有x和y都是关于t的参数方程,求y对x的二阶导数
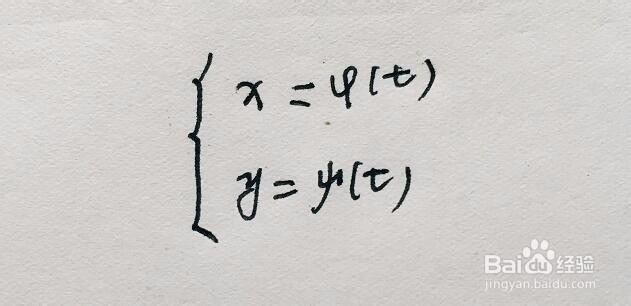 2/3
2/3我们先来求一阶导数:
dy/dx=dy/dt *dt/dx= dy/dt / dx/dt, 所以y对x的一阶导数就等于y对t的一阶导数除以x对t的一阶导数
说明:因为,y和x都是关于t的参数方程,所以求dy/dx时,需要中间增加了dt作为桥梁,使得y和x对t求导。
 3/3
3/3再来求二阶导数:把对x求导转化为对t求导
二阶求导就是把上个步骤我们求出来的一阶导数再次求导,但要记住是对x参数求导,而一阶导数实际上仍然是关于t的方程。所以需要和求一阶导数过程一样的,再次增加dt为桥梁,就变成了一阶导数对t求导再除以x对t求导。如图看过程,主要是红框中增加dt为桥梁的转换,后面就是正常的求导了。
 二、举例子说明1/5
二、举例子说明1/5有如图所示的参数方程
x和y都是关于t的参数方程,求y对x的二阶导数
 2/5
2/5我们先求一阶导数:
一阶导数还是比较容易的,根据上述关于公式的说明中,已经提到,x和y是关于t的参数,所以不能直接求dy/dx,而是增加了dt 来作变换后分别进行y和x对t的求导。
 3/5
3/5上述求导中,将结果进行化解,利用三角函数的一些公式,可以化解得到结果
所以一阶导数就等于cot(t/2)
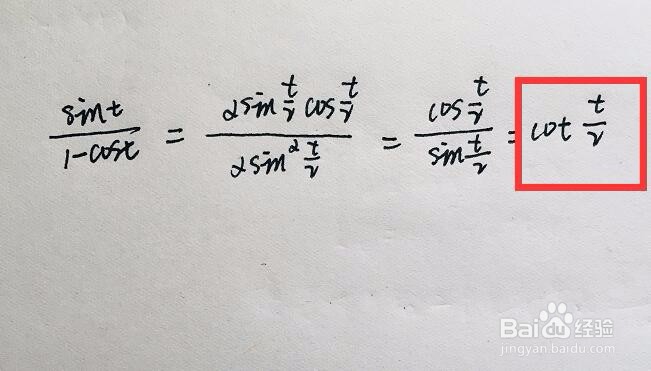 4/5
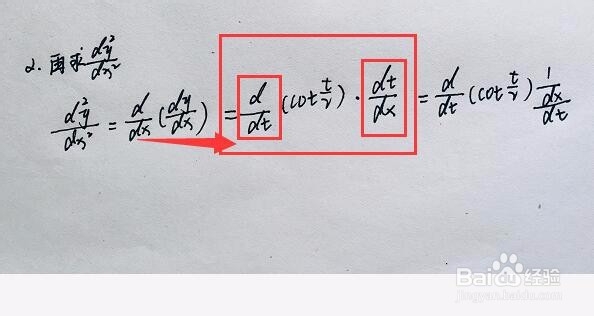
4/5将一阶导数再次求导,牢记分辨参数,这里依然是对x进行再次求导。
而一阶导数cot(t/2)是个关于t的参数,不能对x直接求导,所以继续增加dt为桥梁变换为对t进行求导。
这一步最为关键,很多人会直接把一阶导数cot(t/2) 直接对t求导,就出错了。
 5/5
5/5再往下就简单了,都是对t的正常求导了。
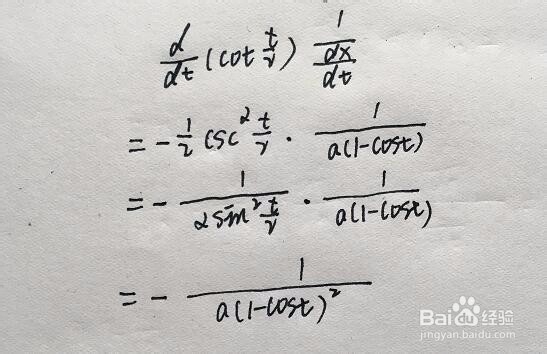 参数方程二阶导数计算方法
参数方程二阶导数计算方法 版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_288263.html
 订阅
订阅