有区别，列举如下：

1、定义不同

导数：当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f（x0）或df（x0）/dx。

极限：某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”（“永远不能够等于A，但是取等于A‘已经足够取得高精度计算结果）的过程。

此变量的变化，被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。

2、本质不同

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”（当然也可以用其他符号表示）。

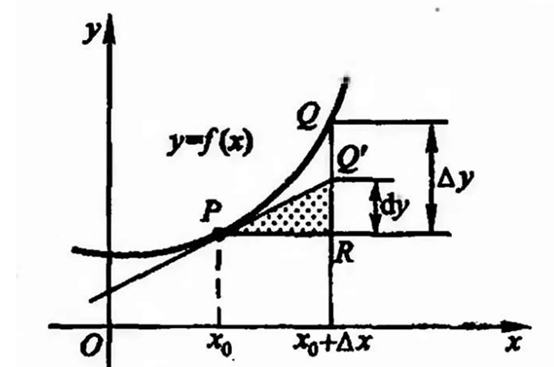
3、起源不同

导数：大约在1629年，法国数学家费马研究了作曲线的切线和求函数极值的方法；1637年左右，他写一篇手稿《求最大值与最小值的方法》。在作切线时，他构造了差分f（A+E）-f（A），发现的因子E就是导数f（A）。

极限：古希腊人的穷竭法蕴含了极限思想，但由于希腊人“对’无限‘的恐惧”，他们避免明显地人为“取极限”，而是借助于间接证法——归谬法来完成了有关的证明。

到了16世纪，荷兰数学家斯泰文在考察三角形重心的过程中，改进了古希腊人的穷竭法，他借助几何直观，大胆地运用极限思想思考问题，放弃了归缪法的证明。如此他就在无意中“指出了把极限方法发展成为一个实用概念的方向”。

4、几何意义不同

如上图所示，导数在图中的直观表现是点P处的直线斜率。

极限的直观表示就是函数图像无限趋近于某一常数但始终达不到，如y=a^x的图像。

参考资料来源：百度百科-导数

参考资料来源：百度百科-极限