不显含x，可令y=p

则y=dp/dx=pdp/dy 代入原方程得

y.*p*dy/dx=-2p^2

dp/-2p=1/y*dy

-1/2lnp=lny+c1

y*p^-1/2=c1*y

c*dy/dx=y^-2

c/y^-2*dy=dx

1/3*c*y^3=x+c1

y^3=c2x+c3

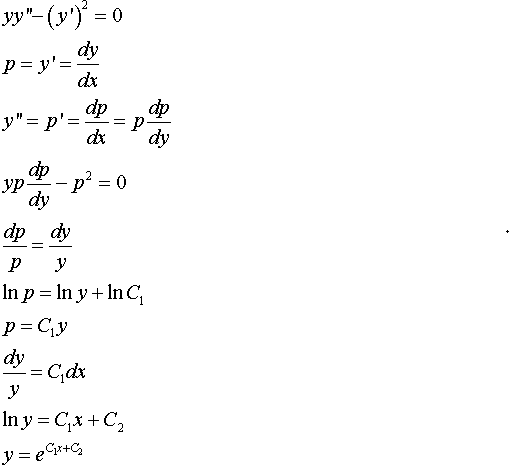
扩展资料：

含义：含有未知函数的导数，如的方程都是微分方程。一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程，叫做微分方程。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的叫做偏微分方程。微分方程有时也简称方程。对于一个微分方程而言，其解往往不止一个，而是有一组，可以表示这一组中所有解的统一形式，称为通解。

求微分方程通解的方法有很多种，如：特征线法，分离变量法及特殊函数法等等。而对于非齐次方程而言，任一个非齐次方程的特解加上一个齐次方程的通解，就可以得到非齐次方程的通解

定义式：f(x,y,y,…``…y(n))=0