MATLAB教学视频：详解数据拟合的MATLAB实现（线性拟合），视频时长约85分钟，通过三个具体的应用案例，详细地讲解了拟合的数学定义，使用拟合方法必备的两个基本条件；重点讲解了使用MATLAB实现线性拟合和多项式拟合的具体步骤和方法，并对典型函数的线性化处理方法，做了详细的介绍。工具/原料moreMATLAB数值计算工具箱MATLAB教学视频：详解数据拟合的MATLAB实现（线性拟合）1/8分步阅读

教学内容

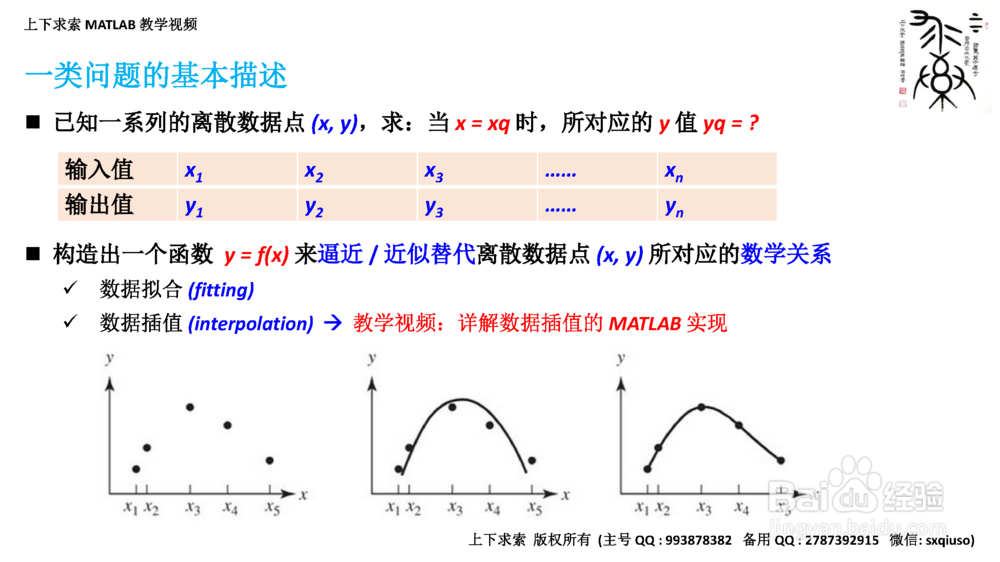
1. 一类问题的基本描述

2. 拟合与插值的区别

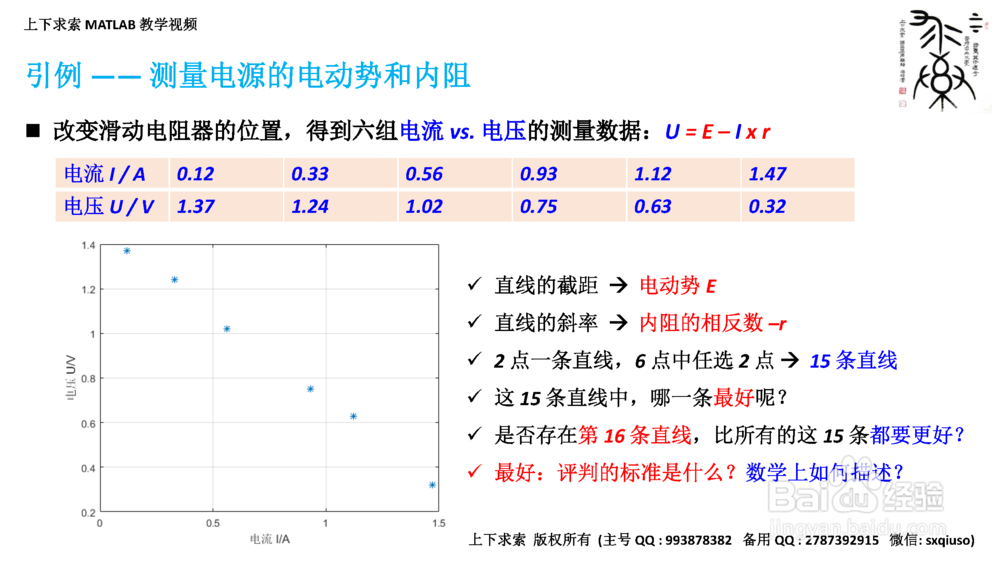
3. 引例——测量电源的电动势和内阻

4. 拟合的数学定义

5. 线性拟合的案例分析

5.1 电源的电动势和内阻

5.2 多项式的拟合

5.3 血药浓度问题

6. 典型函数的线性化处理

2/8

一类问题的基本描述

1.数据拟合

1.1 通过拟合的方法(最小二乘法)，求解出 y = f(x)中的待定参数 a, b

1.2 函数曲线 / 拟合曲线不一定经过所有的已知离散数据点(x, y)

2.数据插值

2.1 选定特定形式的插值函数 y = f(x)，通过插值的方法，求得x和y之间的数学关系

2.2 函数曲线/ 插值曲线一定会经过所有的已知离散数据点(x, y)

3/8

引例——测量电源的电动势和内阻

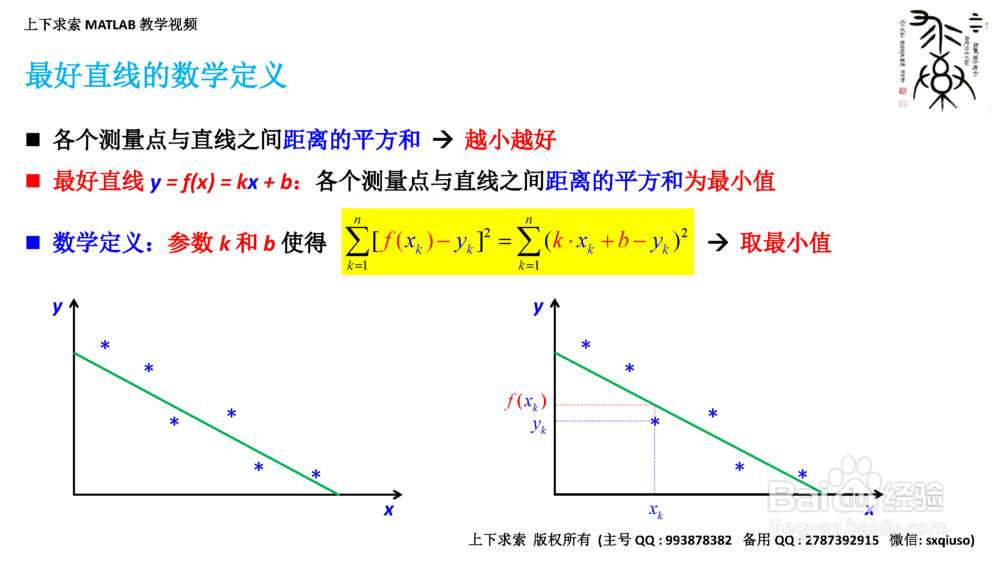
4/8

最好直线的数学定义

1.各个测量点与直线之间距离的平方和：越小越好

2.各个测量点与直线之间距离的平方和为最小值

最小二乘拟合的数学定义

1. 距离的平方和最小：最小二乘法

2. 做拟合算法前，必不可少的两个基本条件

2.1 离散的数据点(x, y)

2.2 数据x y 之间满足的函数关系(参数待定)

5/8

案例一：电源的电动势和内阻

6/8

案例二：多项式的拟合

1.MATLAB 求解线性超定方程组 Ap= B 的最小二乘解：p= A \B 得到拟合多项式的系数

2.MATLAB 自带的多项式拟合函数：p = polyfit(x, y, n)

3.MATLAB 自带的多项式求值函数：y = polyval(p, x)

7/8

案例三：血药浓度问题

8/8

典型函数的线性化处理

针对某些形式函数的拟合问题，可以通过基本的数学变换，转换成线性拟合的问题

注意事项

拟合和插值的数学概念，以及两者之间的联系和区别，务必要搞清楚

能转换成线性拟合问题，优先使用线性拟合的方法