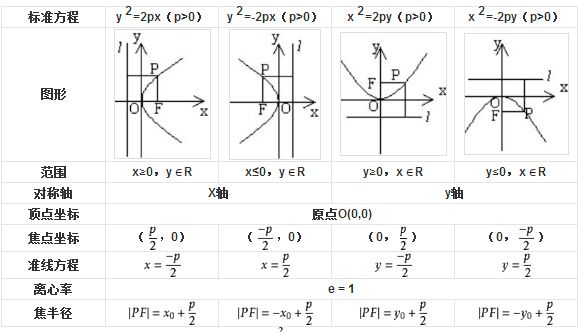
求抛物线y=x^2/2p由顶点到点(根号2p,p)一段弧的长度
来源:网络收集 点击: 时间:2024-03-13【导读】:
对y=2px取导数得 2yy′=2p,故y′=p/y=p/√(2px)
于是弧长S=∫dx=∫√dx
令1+(p/2x)=u,p/2x=u-1,2x/p=1/(u-1),x=p/2(u-1),
当x=0时,u=+∞;
当x=p/2时,u=√2.
dx=-2udu/2(u-1)=-udu/(u-1)
简介
在数学中,抛物线是一个平面曲线,它是镜像对称的,并且当定向大致为U形(如果不同的方向,它仍然是抛物线)。它适用于几个表面上不同的数学描述中的任何一个,这些描述都可以被证明是完全相同的曲线。
抛物线的一个描述涉及一个点(倘墨焦点)和一条线(准线)。焦点并不在准线上。抛物线是该平面中与准线和焦点等距的点的轨迹。抛物线的另一个描述是作为圆锥截面,由圆锥形表面和平行于锥形母线的平面的交点形戴哄成。第三个描述是代数。
垂直于准线并通过焦点的线(即通过中间分解抛物线的线)被称为“对称轴”。与对称轴相交的抛物线上的点被称为“顶点”,并且是抛物线最锋利囊巨施弯曲的点。沿着对称轴测量的顶点和焦点之间的距离是“焦距”。
“直线”是抛物线的平行线,并通过焦点。抛物线可以向上,向下,向左,向右或向另一个任意方向打开。任何抛物线都可以重新定位并重新定位,以适应任何其他抛物线 - 也就是说,所有抛物线都是几何相似的。
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_347789.html
上一篇:煎灌肠
下一篇:拼多多商家版怎么退款
 订阅
订阅