使用BinormalDistribution表示二元正态分布，参数形式为：

计算概率密度函数，表达式如图。

二元正态分布还有其它声明方式。

如图分别是省略均值的方式，和只有相关系数的方式。

它们对应的PDF函数如图。

接下来使用Plot3D绘制二元正态分布的概率密度图像。

带入两个均值为0，x标准差为1，y标准差为2。

相关系数从0变化到0.95。

绘制完毕使用Export导出gif。

这个就是我们绘制的变化图像。当ρ较小时，图像沿着x，y轴都是对称的。

随着相关系数增大，概率密度越来越多的集中在斜线上。

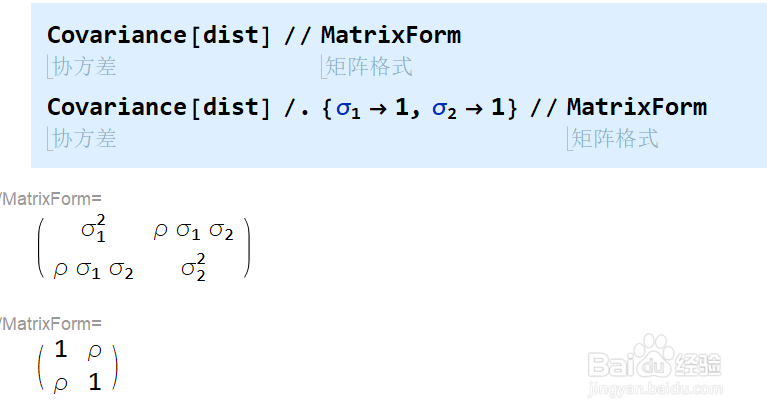
使用Covariance计算协方差矩阵。

当其是标准分布时，协方差矩阵为{{1,ρ},{ρ,1}}。

使用Covariance计算第i个随机变量和第j个随机变量的协方差。

x的方差相当于第一个和第一个，y的方差相当于第二个和第二个。

x和y的协方差相当于第一个和第二个，或者第二个和第一个。

使用Probability计算Y=Y0定值或者X=X0定值时，另一个随机变量的条件分布（累积分布），然后求导得到概率密度。

可见，二元正态分布如果固定一个随机变量，得到的另一个随机变量的条件分布仍然是正态分布。其PDF函数如图。

限于篇幅，本经验未给出二元正态分布其它数字特征的计算。不过一些计算和一元正态分布情形类似，读者可查阅其他资料。

ρ小于零情况类似，只不过分布集中在另外两个象限的直线上。