如何使用几何画板求曲线弧长
来源:网络收集 点击: 时间:2024-03-28求函数f(x)=x³-3x+3在递减区间上的曲线弧长。我们先画出它的图象。单击菜单栏上的图标命令,选择绘制新函数选项,输入函数解析式,确定。
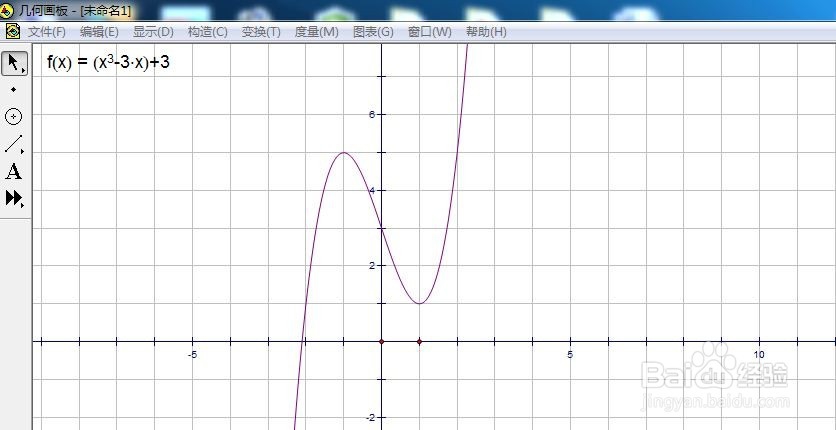 2/8
2/8现在我们来求出它的递减区间。求函数的导数,f′(x)=3x²-3=3(x²-1),显然当x-1,或x1时,f′(x)0,而当-1≤x≤1时,f′(x) ≤0,所以递减区间为。
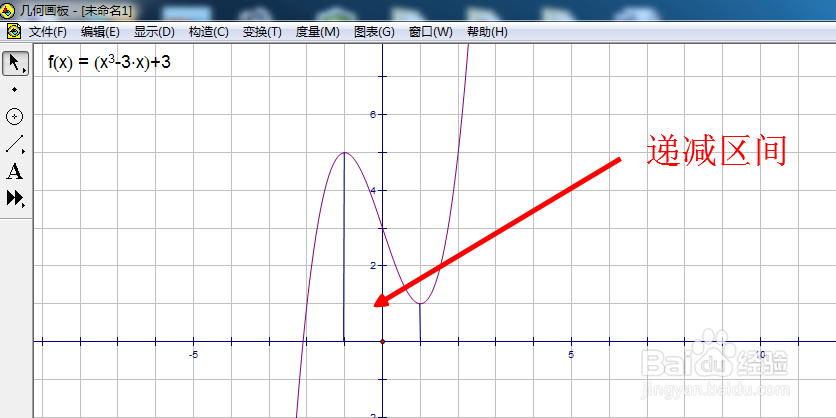 3/8
3/8为了方便求弧长起见,我们先画出递减区间的此获两个端点。先算出端点的纵坐标。单击度量菜单,选择计算。单击函数解析式,输入自变量值,确定。先后算出f(-1)=5,f(1)=1。
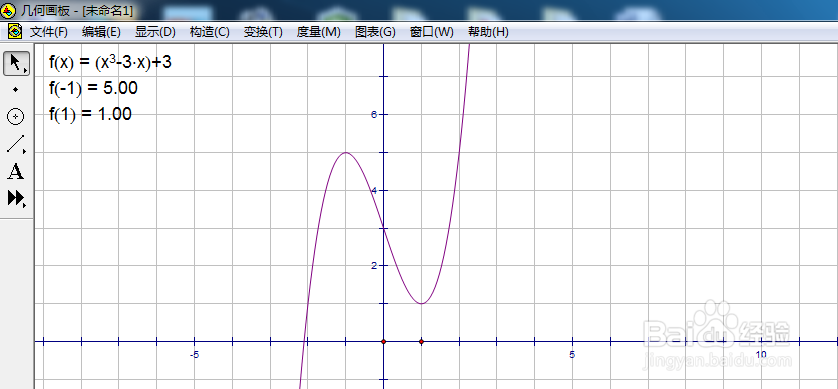 4/8
4/8单击图表菜单,选择绘制点,输入坐标(-1,5),单击绘制,再输入坐标(1,1),单击绘制,然后点帽国劣完成。这样区间端点就画出来了。
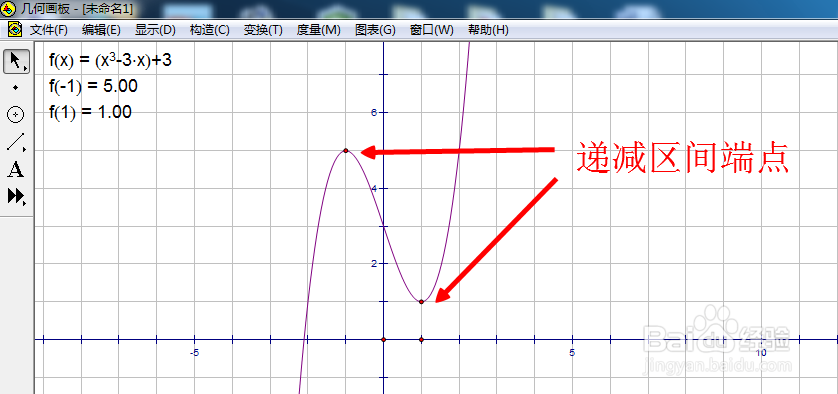 5/8
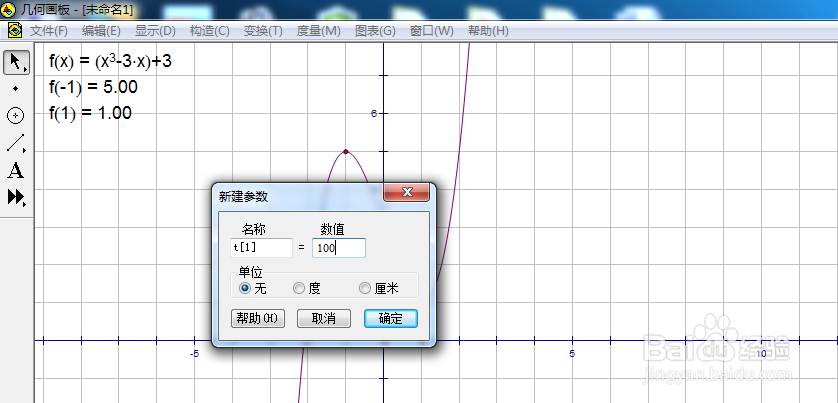
5/8由于计算弧长国诸,需要建立一个参数,我们先完成这项任务。单击图表,选择新建参数,t1=100,确定。
 6/8
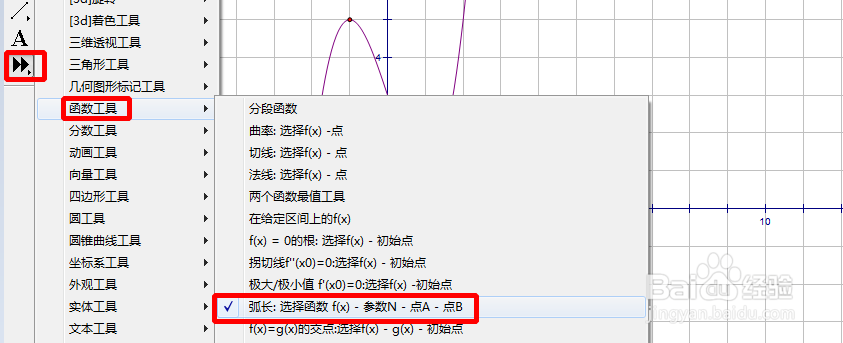
6/8我们还需要设置一下自定义工具。单击自定义工具,选择函数工具,选择弧长,如下图所示。
 7/8
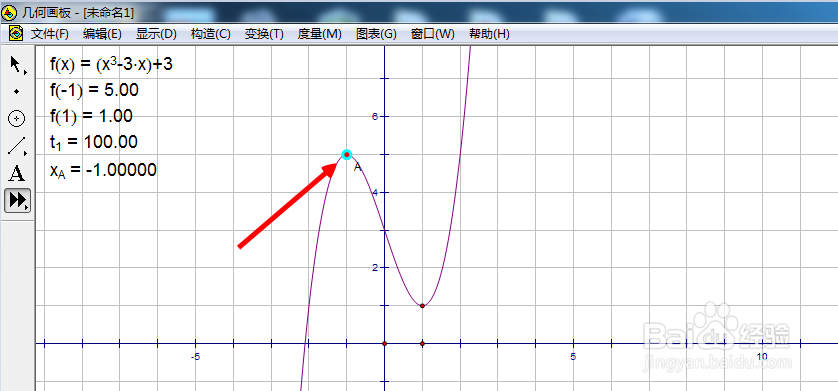
7/8现在来计算弧长,注意操作顺序。单击函数解析式,再单击参数t1,然后移动鼠标,对准递减区间时端点,单击一下。
 8/8
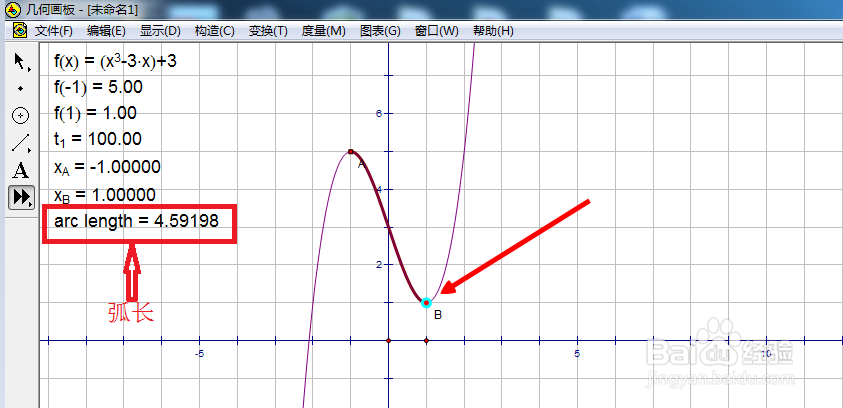
8/8继续移动鼠标,对齐右端点时单击一下。这时,弧长数值就显示出来了。这两步都严格要求对准端点,怎么看对准了没有呢?一是看颜色,点周围出现浅绿色光环,二是看数值,单击时显示的数值和我们求出的端点横坐标相同,这就说明对准了。
 注意事项
注意事项求曲线的弧长要先画出两个端点。
关于参数值的选取请参考其它文章。
学习版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_371057.html
 订阅
订阅