【抽象代数】可逆的Z矩阵
来源:网络收集 点击: 时间:2024-04-02【导读】:
何为Z矩阵?先来说明,所谓的Z指的是整数环。那么,Z矩阵就是元素都是整数的矩阵。特别的,行数和列数相等的Z矩阵,可以称为Z方阵。本文的目标,是要寻找那些可逆的Z矩阵。工具/原料more电脑mathematica网络画板方法/步骤1/6分步阅读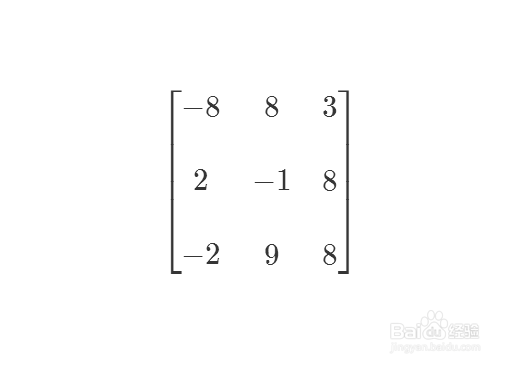 2/6
2/6 3/6
3/6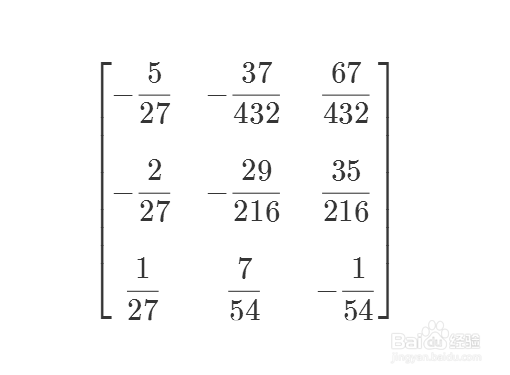 4/6
4/6 5/6
5/6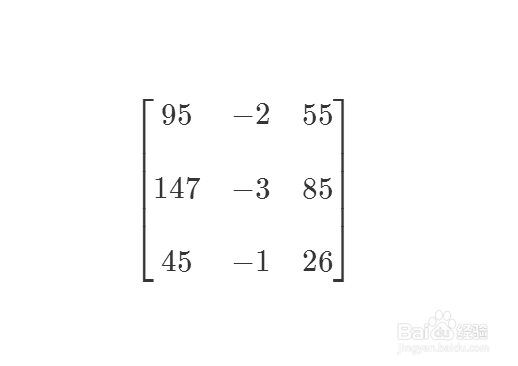 6/6
6/6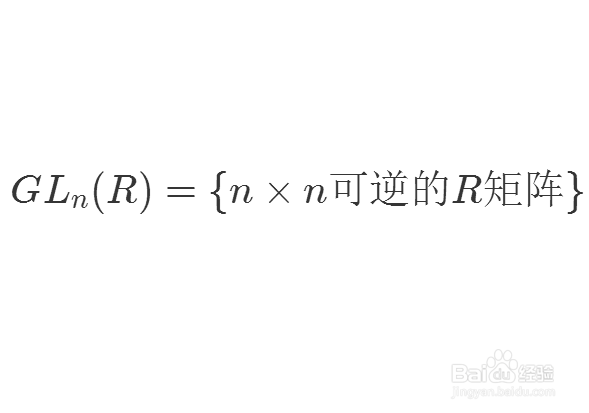
给出一个3*3的Z矩阵。
a=RandomInteger
.
{{-8,8,3},{2,-1,8},{-2,9,8}}
 2/6
2/6在实数范围内,这个矩阵一般是可逆的,除非行列式等于0。
b=Inverse
 3/6
3/6但是,这个逆矩阵已经不是Z矩阵了。
 4/6
4/6如果想要找出在整数范围内可逆的Z矩阵,必须保证矩阵的行列式等于整数环的单位,也就是1或-1。
比如下面的矩阵:
a={{-7,3,5},{-3,5,-10},{12,-5,-9}}
 5/6
5/6上面矩阵的逆矩阵是:
{{95,-2,55},{147,-3,85},{45,-1,26}}
这个矩阵和它的逆矩阵都是Z矩阵。
 6/6
6/6如果把Z矩阵推广到任意环R上面的矩阵,就有了R矩阵的概念。
如果一个R矩阵可逆,那么,这个矩阵的行列式必定等于环R的单位。
所有n阶可逆R矩阵全体,构成了R上的一般线性群。
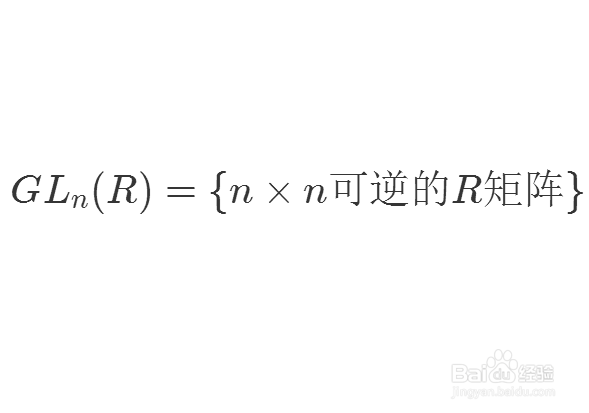
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_400936.html
上一篇:word备份与恢复在哪
下一篇:去法罗群岛周边玩哪些景点值得去
 订阅
订阅