订阅【抽象代数】Z矩阵的对角化
来源：网络收集 点击： 时间：2024-04-02【导读】：
给定一个3*3的Z矩阵。本文，要把这个Z矩阵转化为对角矩阵。在转化的过程中，始终要求矩阵元素都是整数。工具/原料more电脑mathematica方法/步骤1/8分步阅读
2/8
3/8
4/8
5/8
6/8
7/8
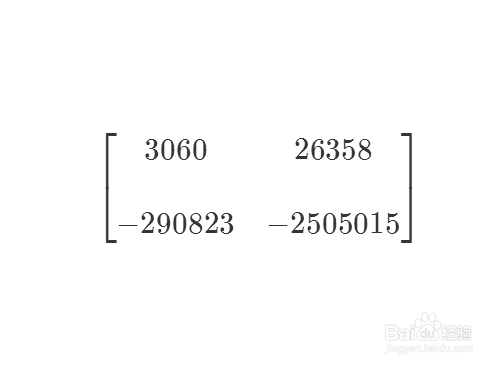
8/8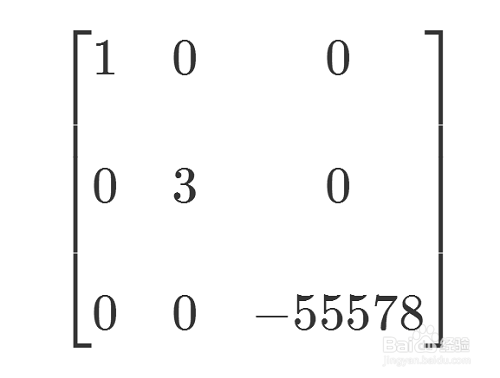
随机矩阵：
a=RandomInteger
2/8通过行置换和列置换，把最小的元素移动到左上角。
b={a],a],a]}\;
c={b],b],b]}\;
3/8用第二行重复减去（或加上）第一行，直到第二行第一个元素变成了最小的正整数。
c]=c]-c]*Floor]/c]];
4/8新的矩阵，第二行第一个元素如果不是0，就需要重复步骤1，把绝对值最小的非0数字置于左上角。
b=c;c={b],b],b]}
5/8然后重复步骤2。
如果第二行的第一个元素变成了0，那么对第三行执行同样的操作。如果第三行第一个元素不等于0，还得重复步骤1和步骤2，直到矩阵的第一列只有第一个元素不等于0。
6/8用上面同样的方法，把矩阵的第一行变成只有第一个元素非零。
这样，第一行和第一列，只有对角元素非0。
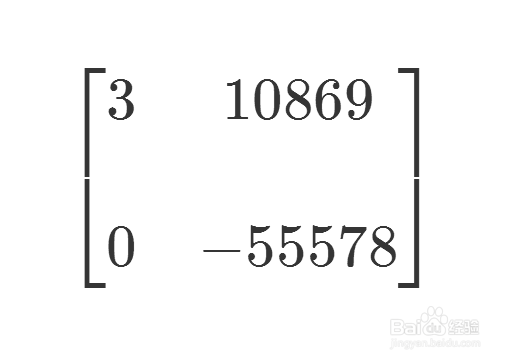
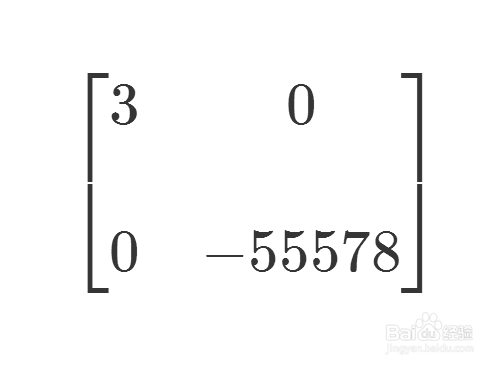
7/8然后对剩下的块矩阵执行上面的操作，最后把原来的矩阵变成了一个对角矩阵。
8/8两个矩阵的行列式相等。
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_401341.html
上一篇：普通话证书丢了怎么查编号
下一篇：oppo手机怎样给软件加密码教程
