证明：依题n≥3，说明所有小于等于N的质数一定包括2和3。下面先证如下假设：Bertrand 假设： 对任意自然数 n ≥ 2， 至少存在一个素数 p 使得 n lt; p lt; 2n。

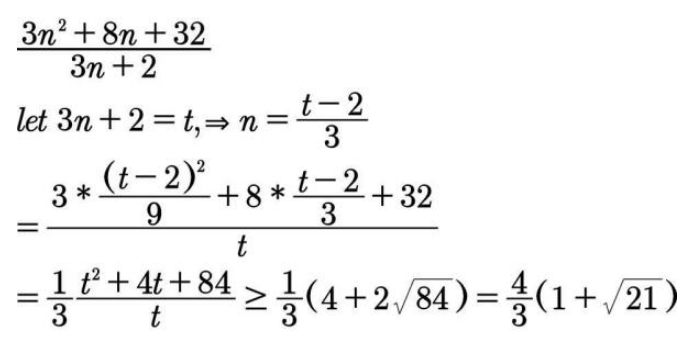
在证明 Bertrand 假设前我们先来证明几个辅助命题。

引理 1： 设 n 为一自然数， p 为一素数， 则能整除 n! 的 p 的最高幂次为： s = Σi≥1floor(n/pi) (式中 floor(x) 为不大于 x 的最大整数)。

证明： 能整除 n! 的 p 的最高幂次显然等于从 1 到 n 的各自然数中 p 的最高幂次之和， 即 s = Σ1≤i≤n si (其中 si 为能整除 i 的 p 的最高幂次)。 现在将从 1 到 n 的所有 (n 个) 自然数排列在一条直线上， 在每个数字上叠放一列 si 个记号， 显然记号的总数是 s。

关系式 s = Σ1≤i≤n si 表示的是先计算各列的记号数 (即 si) 再求和。 但我们也可以先计算各行的记号数再求和， 由此得到的关系式正是引理 1。

为了证明这一点， 我们从数字所在的直线开始自下而上计数。 很明显所有第一行有记号的数字都含有因子 p (因为否则的话 si = 0， 没有记号)， 这种数字的总数 (也就是该行的记号总数) 是 floor(n/p)。

第二行有记号的数字都含有因子 p2 (因为否则的话 si lt; 2， 在第二行上不会有记号)， 这种数字的总数 (也就是该行的记号总数) 是 floor(n/p2)， 依此类推， 第 i 行的记号总数为 floor(n/pi)。 将所有这些数字相加便证明了引理 1。