【抽象代数】有理数环的扩张
来源:网络收集 点击: 时间:2024-04-06【导读】:
有理数Q在加法和乘法下,形成一个环。如果引进新的元素x和y,其中x=sqrt{2},y=sqrt{3},可以把有理数环扩展为新的环。工具/原料more电脑python方法/步骤1/7分步阅读 2/7
2/7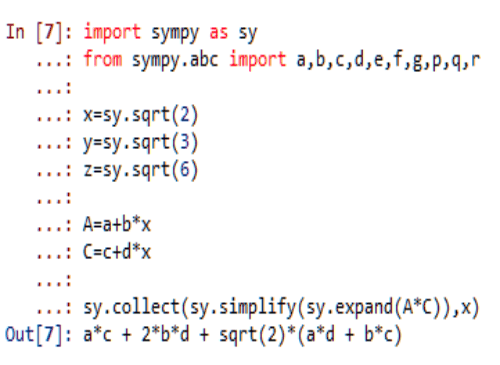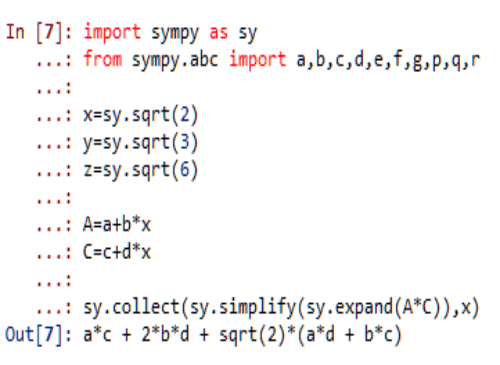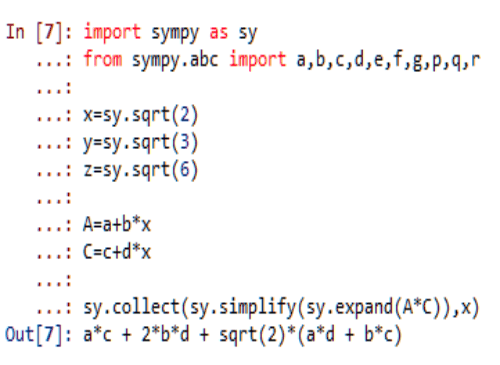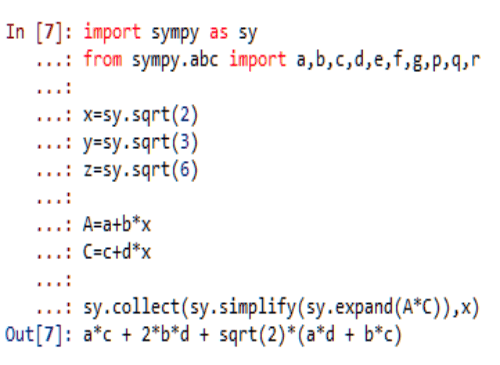 3/7
3/7 4/7
4/7 5/7
5/7 6/7
6/7
 7/7
7/7
Q和x组合,得到环Q。
 2/7
2/7对Q里面的任意两个元素,进行加、减、乘,结果仍旧属于Q。
以乘法为例,如果a、b、c、d都是有理数,那么,
a*c + 2*b*d 和 a*d + b*c 也都是有理数。
 3/7
3/7y=sqrt{3}。
如果把Q和y组合,会得到什么结果?
 4/7
4/7我们要求出Q里面的元素的一般形式。
 5/7
5/7如果假设:
x=sqrt(2)
y=sqrt(3)
z=sqrt(6)
那么,Q里面的元素的一般形式可以表示为:
 6/7
6/7假设w=sqrt(2)+sqrt(3)。可以发现,Q=Q=Q。

 7/7
7/7不过,这是需要证明的。只需要证明,下面的方程组里面有有理数解就可以。
其中,a、b、c、d是已知的有理数,而e、f、h、p、q、s则视为未知数。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_439592.html
上一篇:网格登记居住信息怎么查
下一篇:Windows11怎么关闭屏保
 订阅
订阅