【平面几何】一个等角的尺规作图问题
来源:网络收集 点击: 时间:2024-04-07【导读】:
△ABC中,ACAB,M、N分别是AB、BC的中点。要求在线段MN上找X点,使得∠ABX=∠ACX。本文,就给出这个问题的尺规作图方法。工具/原料more电脑网络画板方法/步骤1/7分步阅读 2/7
2/7 3/7
3/7 4/7
4/7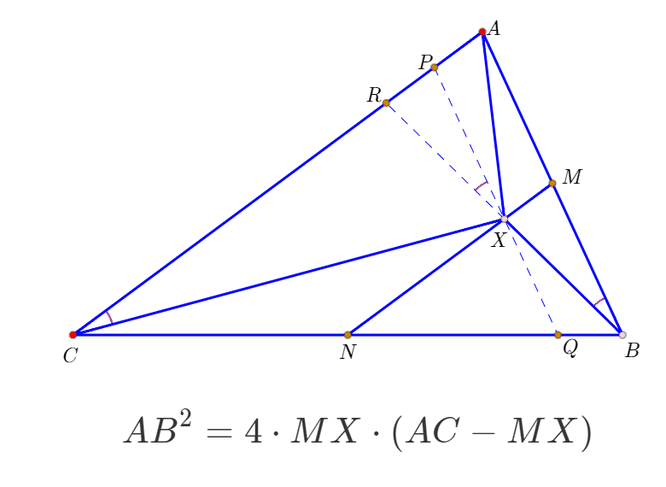 5/7
5/7 6/7
6/7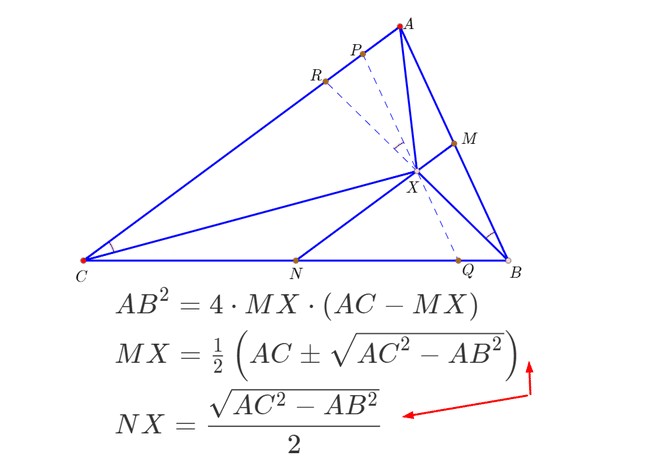 7/7
7/7
设BX的延长线交AC于R,那么X就是BR的中点,AR=2MX。
 2/7
2/7过X作AB的平行线,交AC、BC于P、Q,那么,P是AR中点。
 3/7
3/7注意角度相等的关系,可以得出结论:PX^2=PR*PC。
 4/7
4/7注意到PX=AB/2,PC=AC-AP=AC-PR=AC-MX,所以得到如下关系:
AB^2=4*MX*(AC-MX)
 5/7
5/7解这个关于MX的方程,得到两个解:
 6/7
6/7这两个解有一个大于AC/2,不符合题意,只能保留较小的那个解。
由此可以求出NX的大小:
 7/7
7/7注意到ACAB,所以点X始终位于MN之间。
以N为圆心、sqrt(AC^2-AB^2)/2为半径作圆,与线段MN的交点,即为X点。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_453095.html
上一篇:简单吊牌的设计
下一篇:欢乐斗地主如何设置在线状态
 订阅
订阅