MATLAB教学视频：傅里叶变换的频域滤波详解，视频时长约80分钟，通过实例讲解和MATLAB代码的编写，详细解释了频域滤波的基本方法和实施步骤，让同学们加深理解时域和频率之间的转换，同时，建立起系统对输入信号响应的概念。基本原理：系统对输入信号的稳态响应，可以先通过傅里叶变换FFT，在频域内进行计算，再反傅里叶变换IFFT，得到时域的输出信号。常常被忽视的内容：傅里叶FFT频谱图的共轭对称性工具/原料moreMATLAB信号处理工具箱MATLAB教学视频：傅里叶变换的频域滤波详解1/2分步阅读

教学内容

1. 系统对输入的响应(稳态)

2. 信号通过理想低通滤波器

3. 信号通过RC 低通滤波器

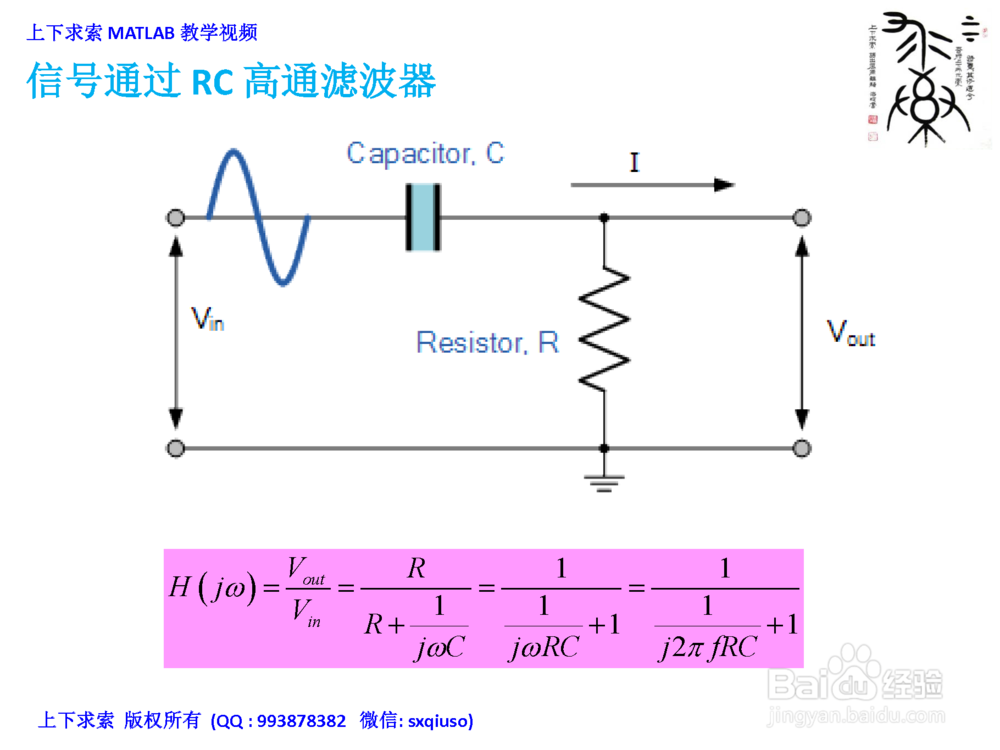
4. 信号通过RC 高通滤波器

2/2

系统对输入的响应(稳态)

x(t)：输入信号(时域)

X(jω)：输入信号的傅里叶变换(频域)

H(jω)：系统的频率响应

Y(jω)：输出信号的傅里叶变换(频域)

y(t)：输出信号(时域)

对Y(jω)做傅里叶反变换，得到时域输出信号y(t)

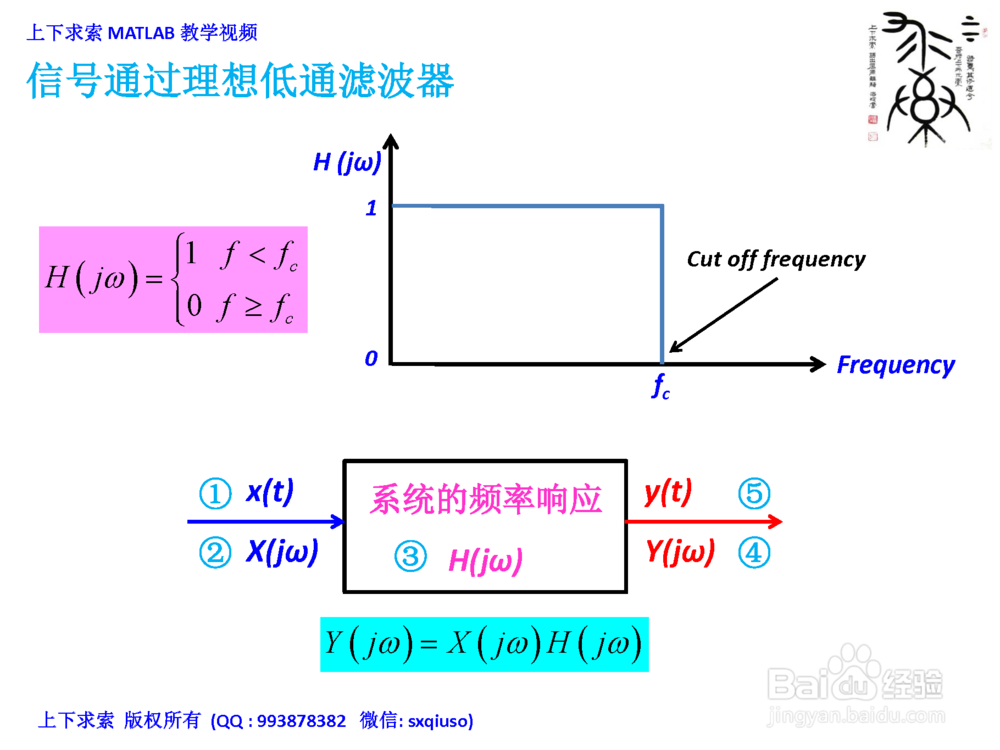
信号通过理想低通滤波器1/4

信号通过理想低通滤波器后，输出的时域信号

求解一个信号x(t)通过一截止频率为50Hz的理想低通滤波器后，输出的时域信号y(t)

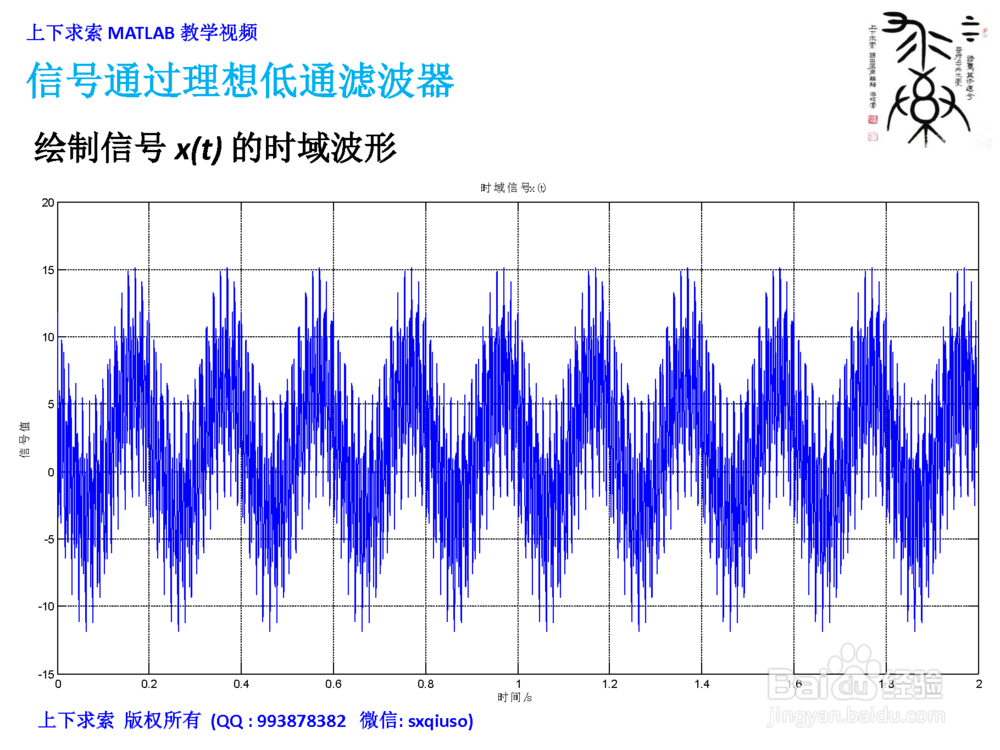
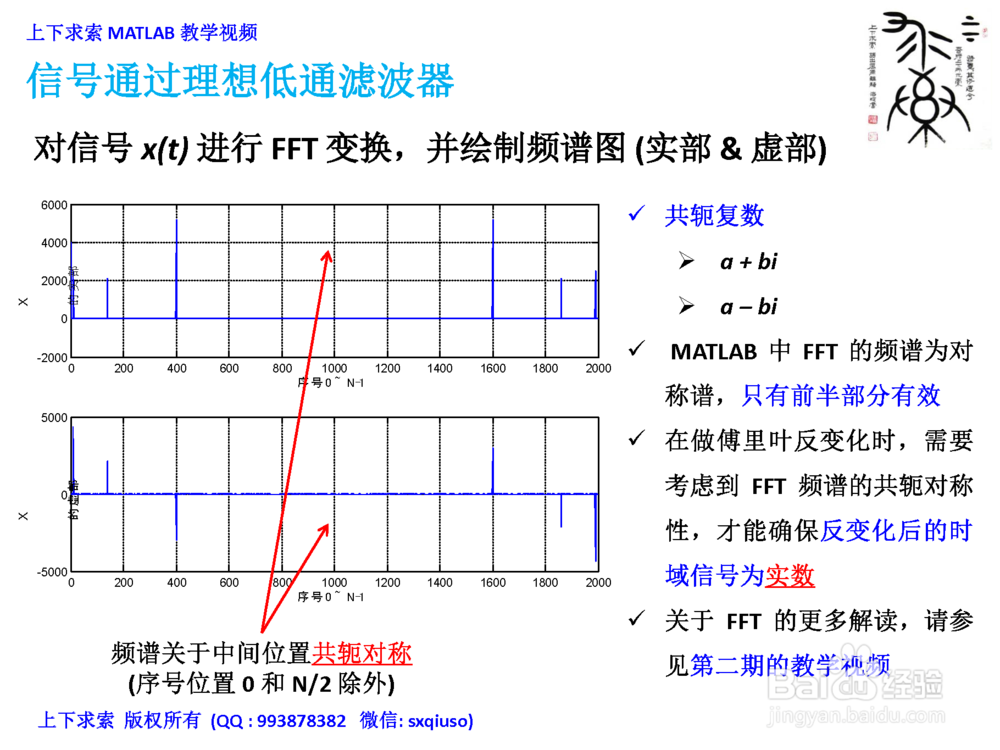
2/4

绘制信号FFT频谱，考察频谱的对称性

在MATLAB里绘制信号x(t)的时域波形，对信号x(t)进行FFT变换，并绘制频谱图 (实部虚部)

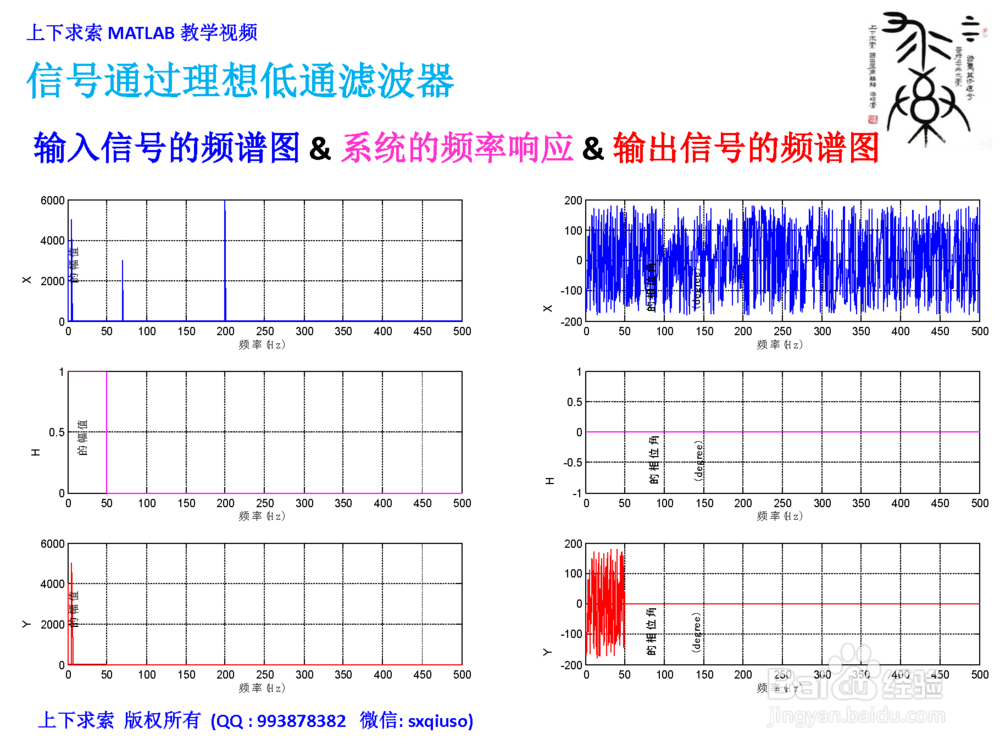
3/4

在MATLAB里计算并绘制

1. 输入信号的频谱图

2. 系统的频率响应

3. 输出信号的频谱图

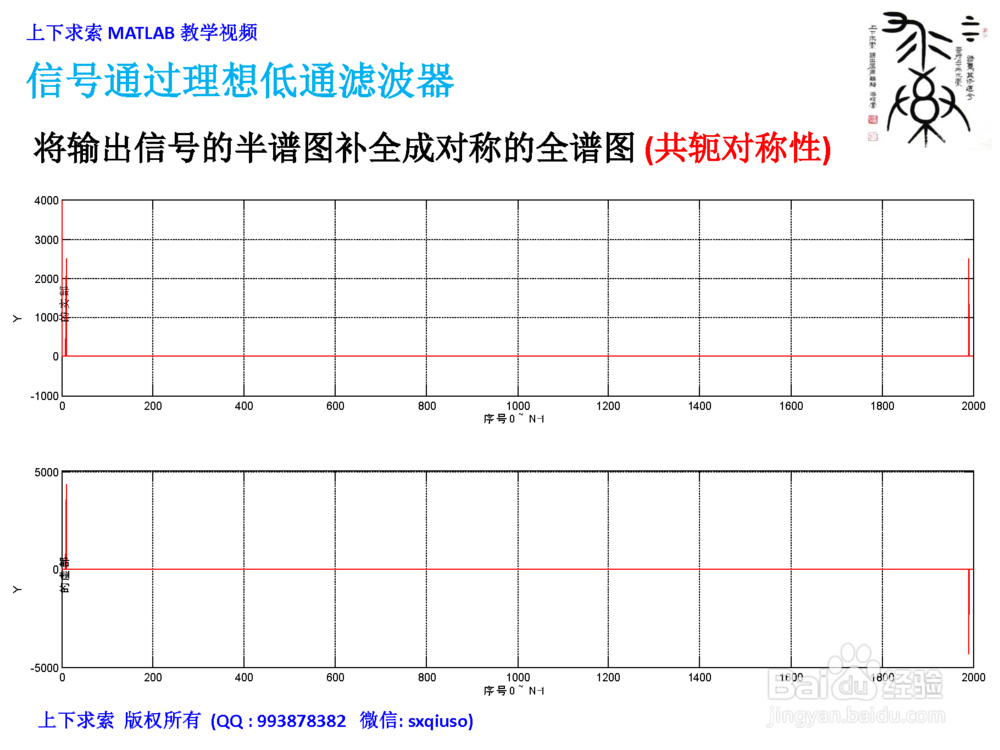
4/4

将输出信号的半谱图补全成对称的全谱图 (共轭对称性)

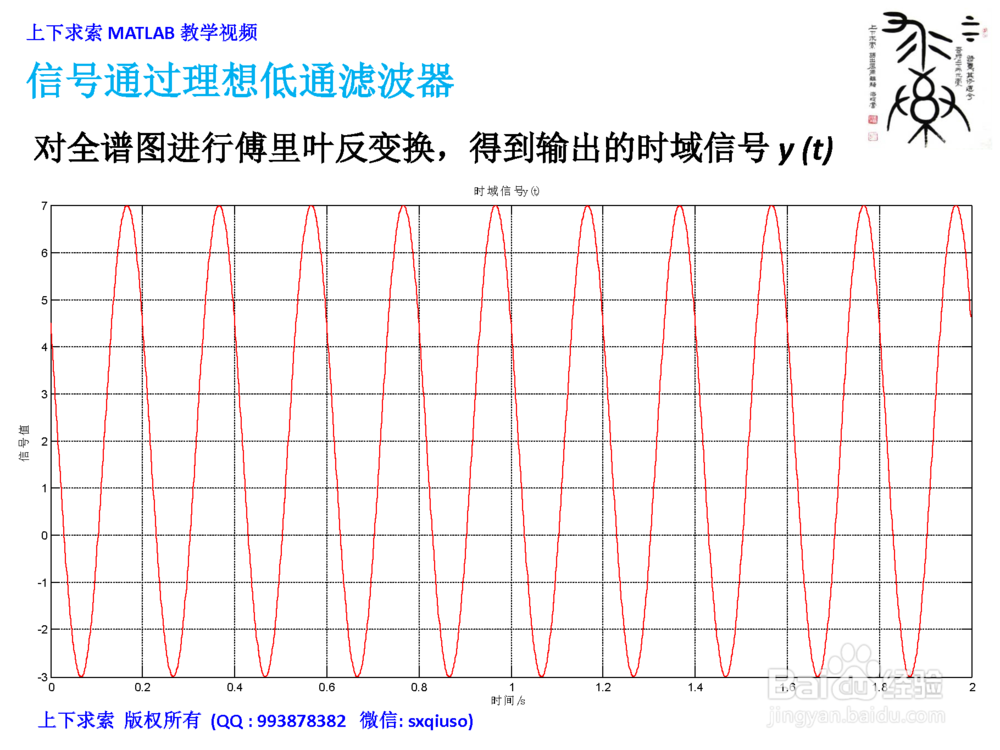
对全谱图进行傅里叶反变换IFFT，得到输出的时域信号y(t)

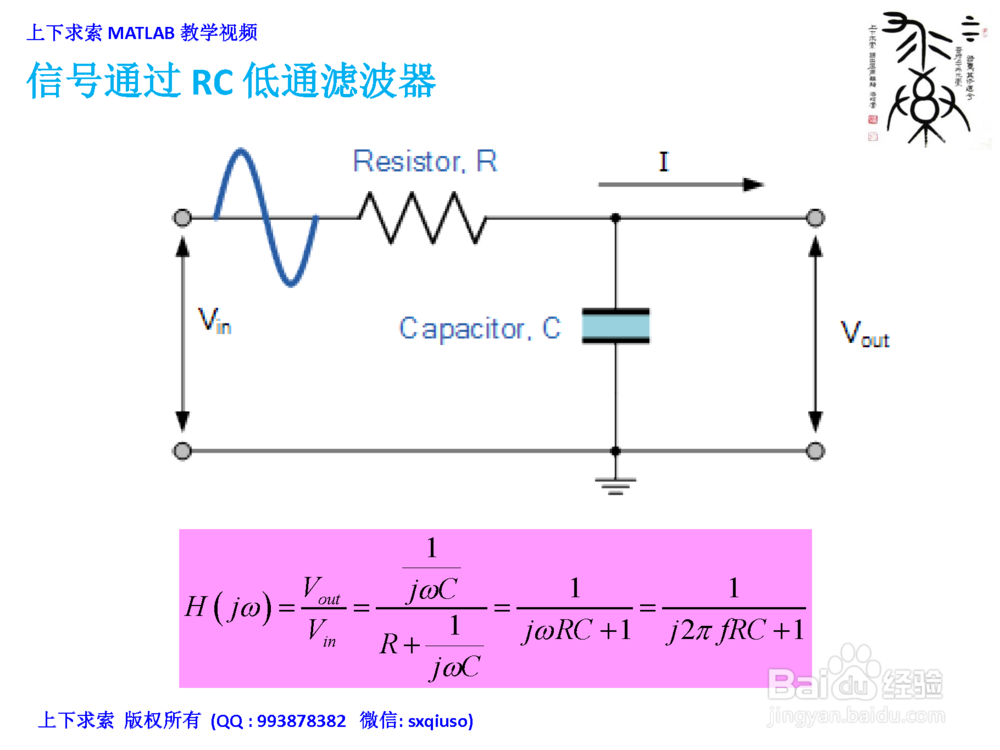
信号通过RC低通滤波器1/3

绘制方波信号x(t)=square(5πt)的时域波形

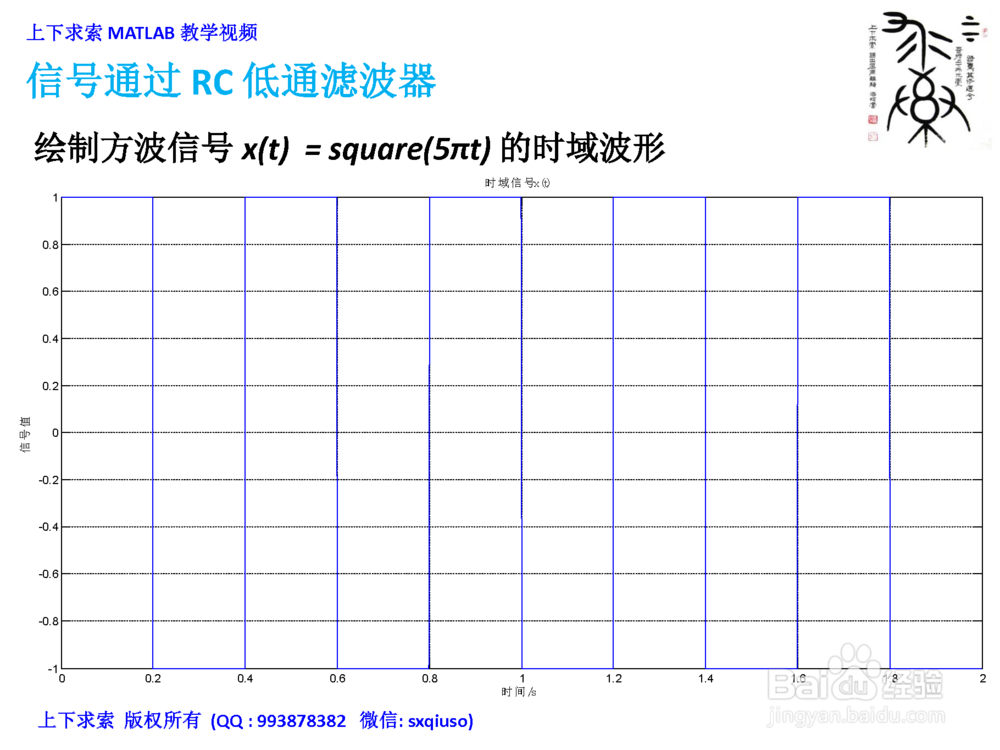2/3

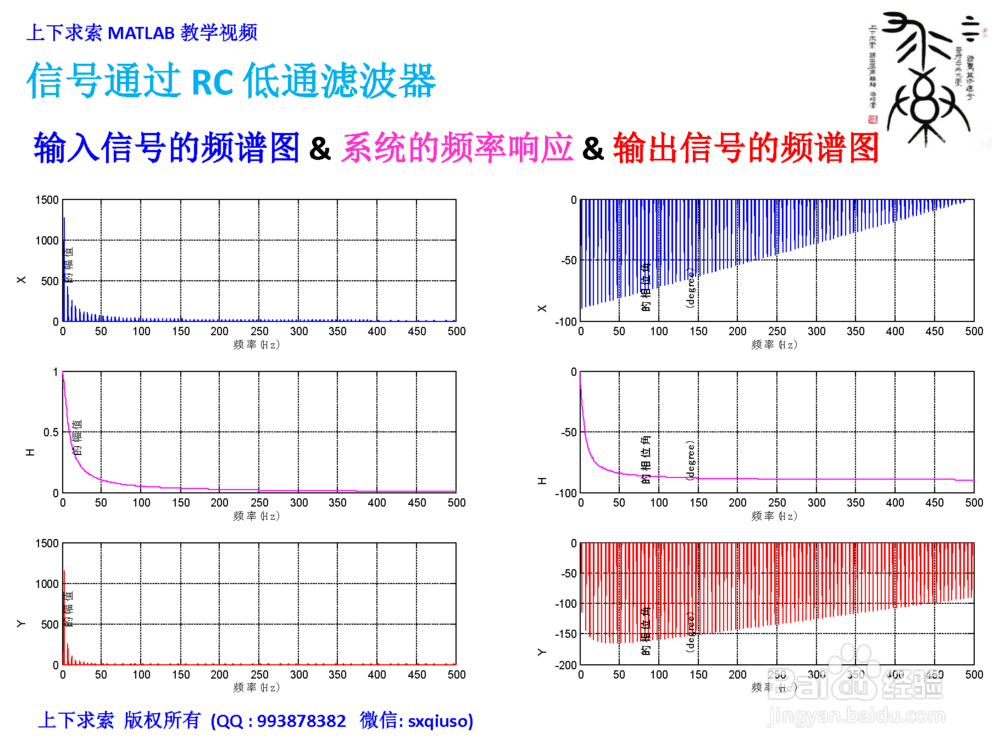
在MATLAB里计算并绘制

1. 输入信号的频谱图

2. 系统的频率响应

3. 输出信号的频谱图

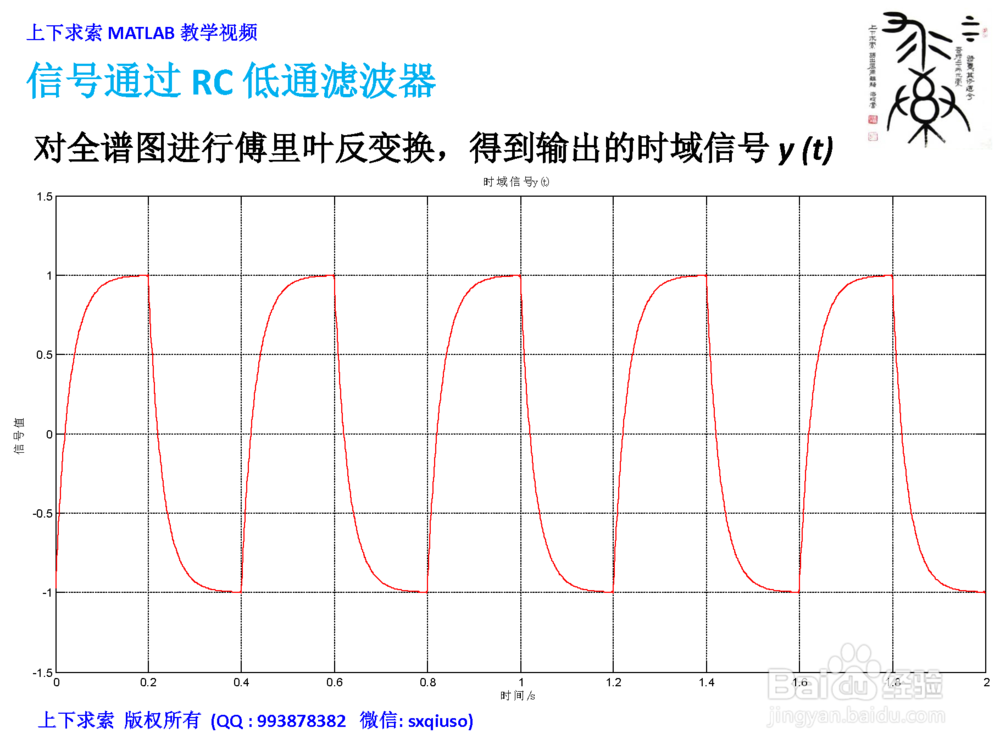
3/3

对全谱图进行傅里叶反变换IFFT，得到输出的时域信号y(t)

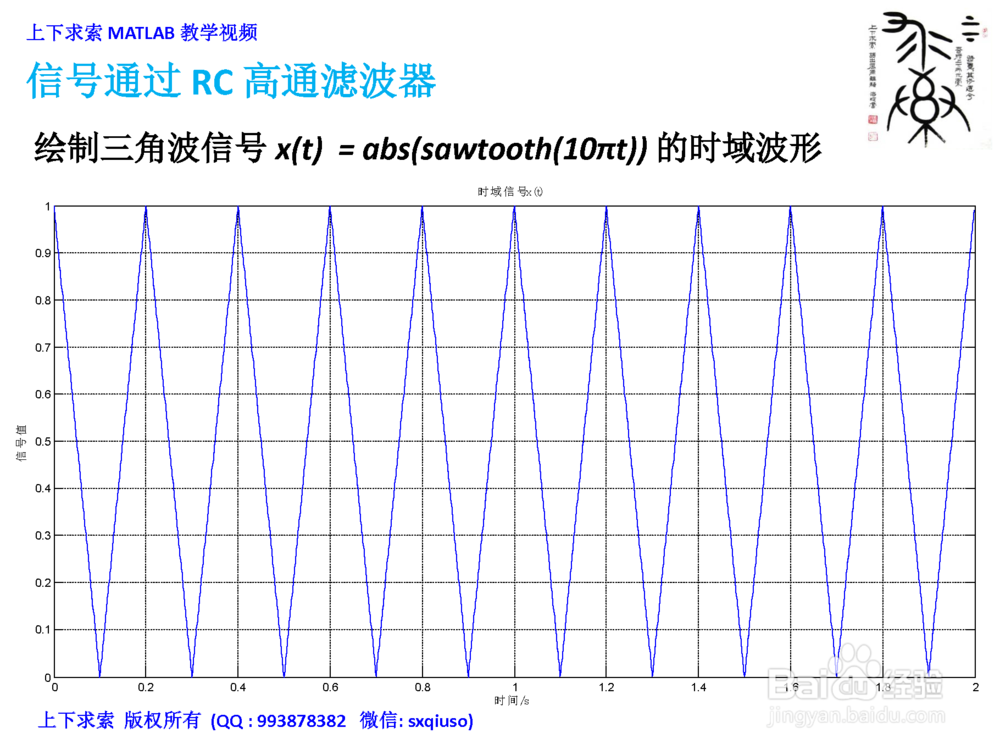
信号通过RC高通滤波器1/3

绘制三角波信号x(t)=abs(sawtooth(10πt))的时域波形

2/3

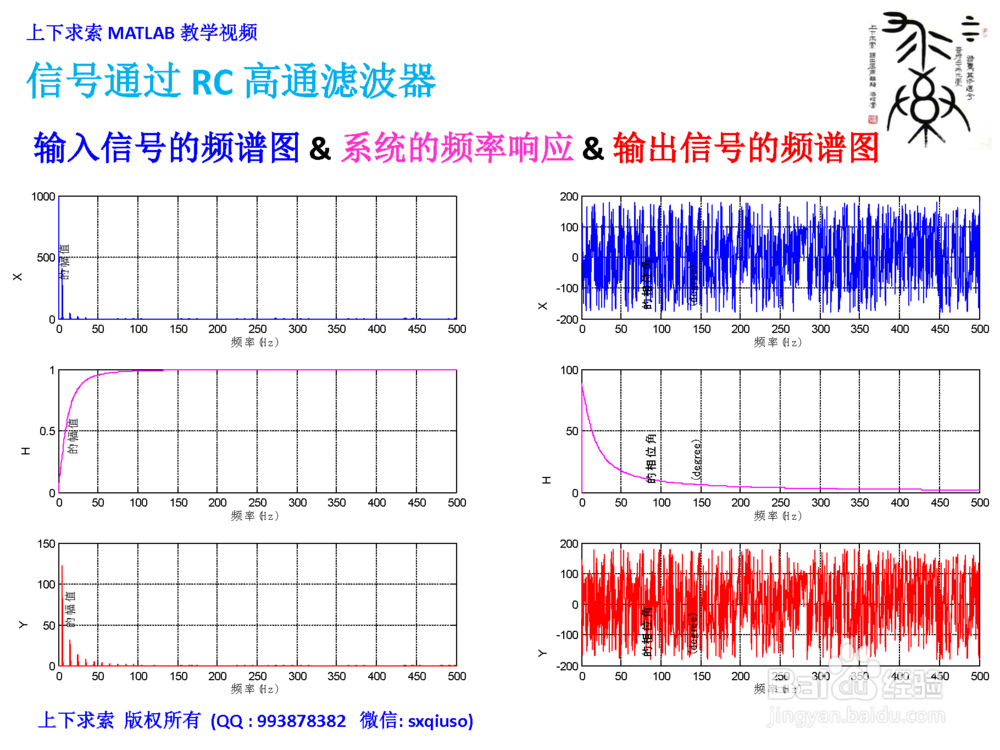
在MATLAB里计算并绘制

1. 输入信号的频谱图

2. 系统的频率响应

3. 输出信号的频谱图

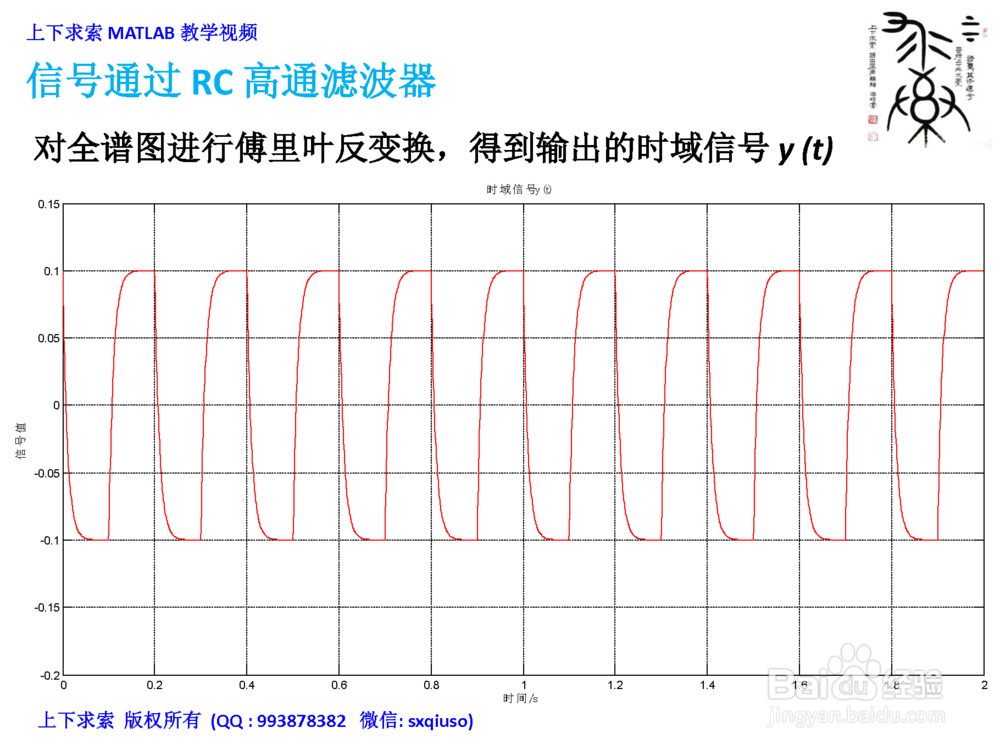
3/3

对全谱图进行傅里叶反变换IFFT，得到输出的时域信号y(t)

注意事项

信号与系统的专业知识是基础

MATLAB是处理问题的工具

FFT频谱的共轭对称性，千万不可忽视