订阅画复合分式函数y=(3x³-2)/(x+1)³图像的主要步骤
来源：网络收集 点击： 时间：2024-04-17根据分数函数的定义要求，必须分母整体不为0，则x+1≠0，即可知函数自变量的取值，进一步可写出函数的定义域。
2/2在高中数学里，定义域的定义为：设A，B是两个非空的数集，如果按某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f:A--B为集合A到集合B的一个函数，记作y=f(x)，x属于集合A。其中，x叫作自变量，x的取值范围A叫作函数的定义域。
函数的单调性1/2函数的单调性是函数的重要性质，反映了随着自变量的增加函数值的变化趋势，它是研究函数性质的有力工具，在解决比较大小、解决函数图像、值域、最值、不等式问题都有很重要的作用。
2/2如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f(x)0，则函数y=f(x)在区间D内单调增加;反之，若x∈D时，f(x)0,则称函数y=f(x)在区间D内单调减少。
函数的凸凹性1/2通过函数的二阶导数，解析函数的凸凹区间。
2/2如果函数f(x)在区间I上二阶可导，则f(x)在区间I上是凸函数的充要条件是f(x)=0。
函数的极值1/2计算函数在无穷远处和函数的点断点处的极限：
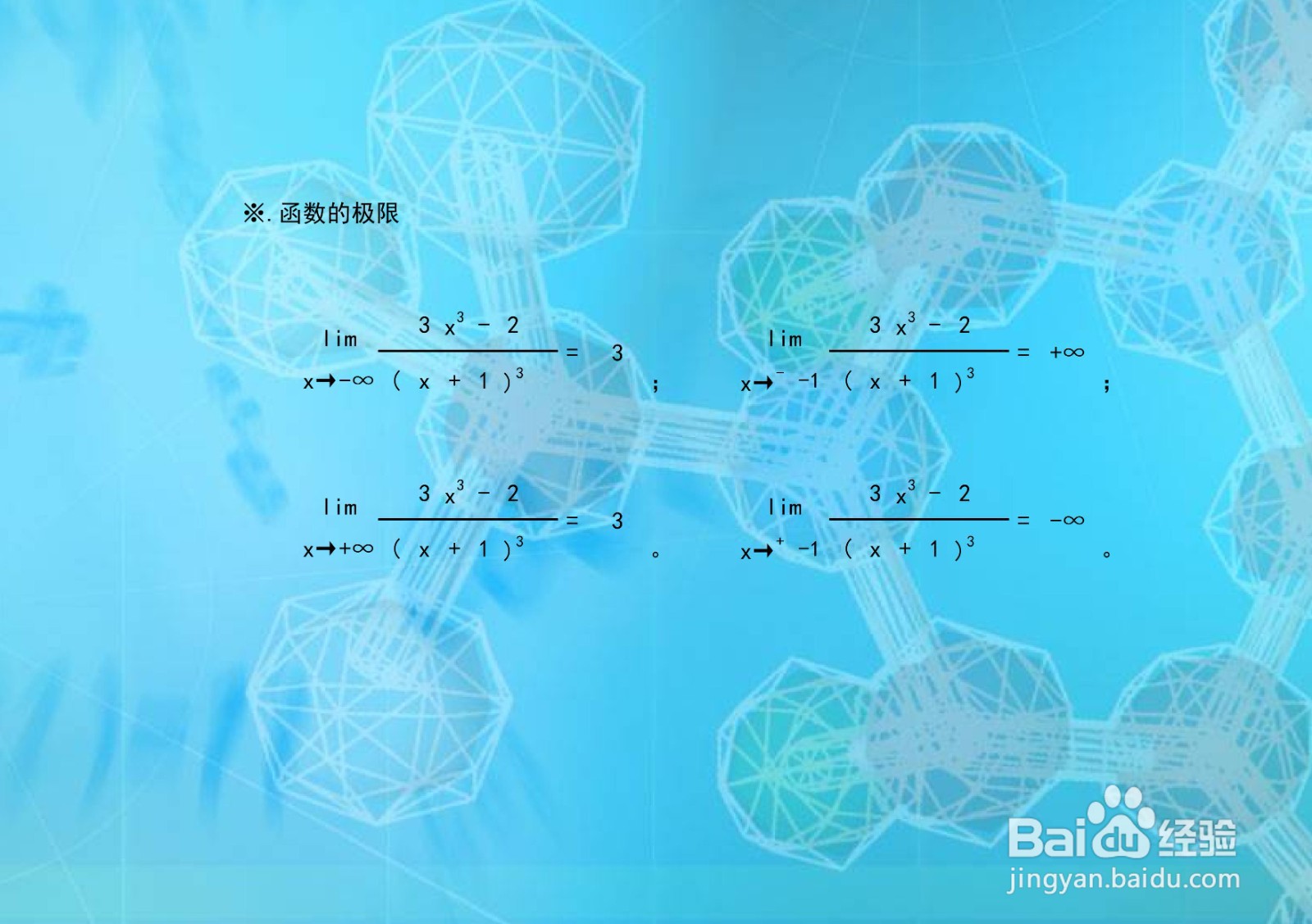2/2极限指某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”，极限是一种“变化状态”的描述。
函数的示意图1/2根据函数单调性、凸凹性等性质，列举函数在定义域区间上部分关键点坐标。
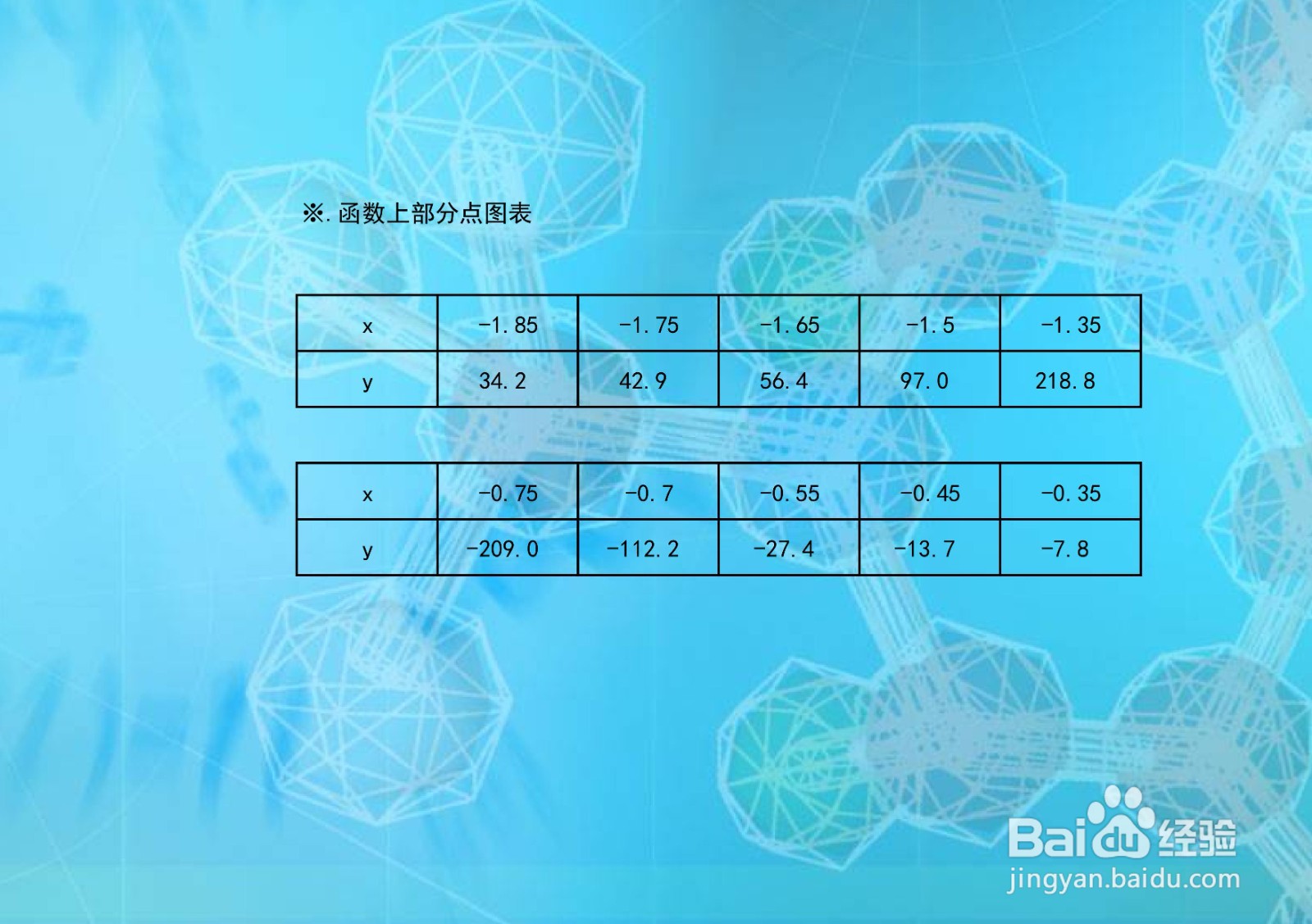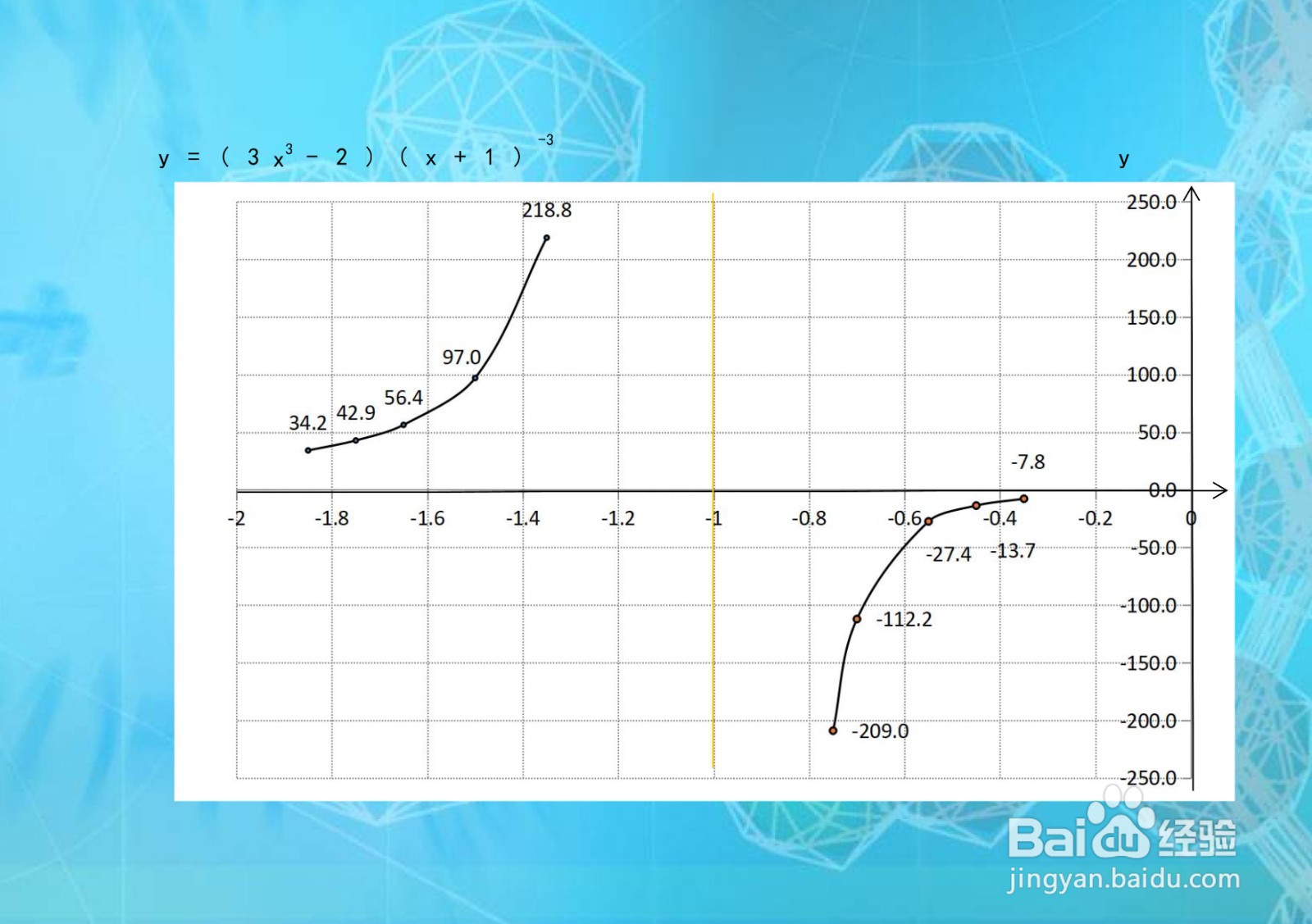
2/2综合以上函数的定义域、单调性、凸凹性、极限性质，并结合函数的定义区间和单调、凸凹区间，即可画出函数的示意图如下：
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_534360.html
