Mathematica如何用拉普拉斯变换解微分方程?
来源:网络收集 点击: 时间:2024-04-18【导读】:
介绍Mathematica中的拉普拉斯变换,拉普拉斯逆变换,以及如何方便的解微分方程。工具/原料moreMathematica 11.0方法/步骤1/8分步阅读 2/8
2/8 3/8
3/8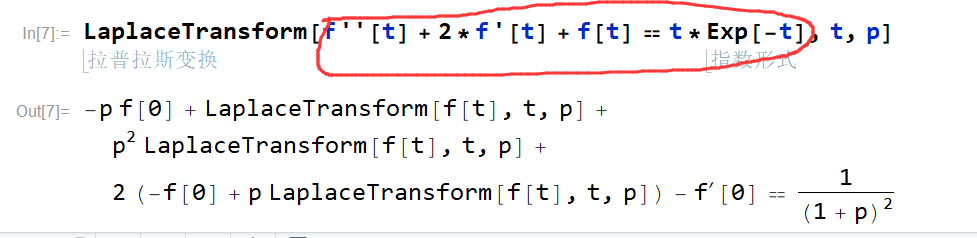 4/8
4/8 5/8
5/8 6/8
6/8 7/8
7/8 8/8
8/8 注意事项
注意事项
首先,使用LaplaceTransform函数可以求出函数的拉普拉斯变换,使用InverseLaplaceTransform函数可以求出逆变换。
第二个和第三个参数分别为本(像)函数变元和像(本)函数变元。
 2/8
2/8我们可以在LaplaceTransform的待变换函数中添加自定义函数,和函数的导数等等,它们都可以被正确变换。
 3/8
3/8使用LaplaceTransform函数可以直接对一个等式(微分方程)进行拉普拉斯变换,如图所示。由于是微分方程,f未定义,变换结果仍带有LaplaceTransform
 4/8
4/8我们可以使用 /.{替换列表} 来替换f,f和LaplaceTransform,t,p],就好比带入初始值,设f的像函数为F。
替换成一个可解的方程,如图。
 5/8
5/8使用Solve函数对该方程求F的解,如图。
 6/8
6/8接着对得到的解使用InverseLaplaceTransform求其逆变换,得到原微分方程的解。
 7/8
7/8为了验证结果,我们使用DSolve函数求解该微分方程,可以看到同样结果。
 8/8
8/8LaplaceTransform函数同样可以在Wolfram Alpha上使用。
 注意事项
注意事项对微分方程进行Laplace变换后,我们也可以不替换带入初始值,直接尝试Solve并逆变换出方程的通解。
MATHEMATICA拉普拉斯变换复变函数微分方程版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_535518.html
上一篇:淘宝下单发货地址如何查看
下一篇:女朋友出轨了怎么办
 订阅
订阅