【抽象代数】Gauss整数环里面的最大公约数
来源:网络收集 点击: 时间:2024-01-24【导读】:
本文,介绍Gauss整数环里面,最大公约数的计算方法——Euclid算法。工具/原料more电脑网络画板方法/步骤1/5分步阅读 2/5
2/5 3/5
3/5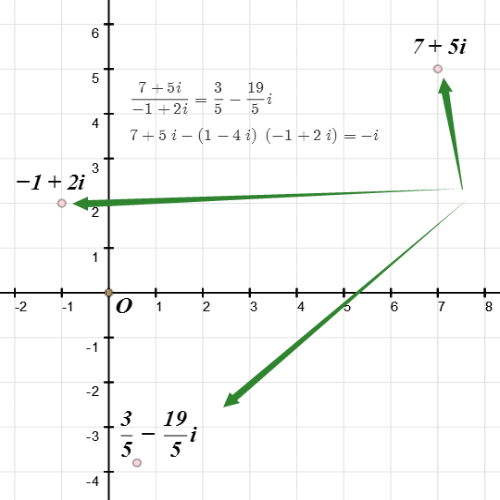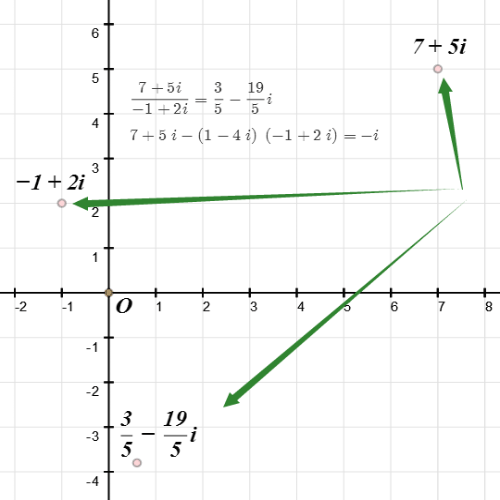 4/5
4/5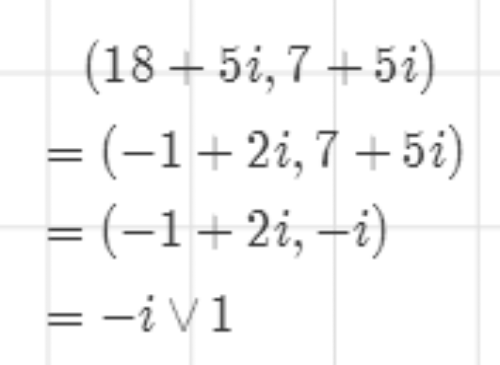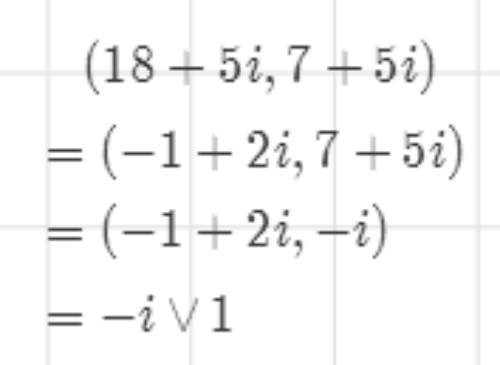 5/5
5/5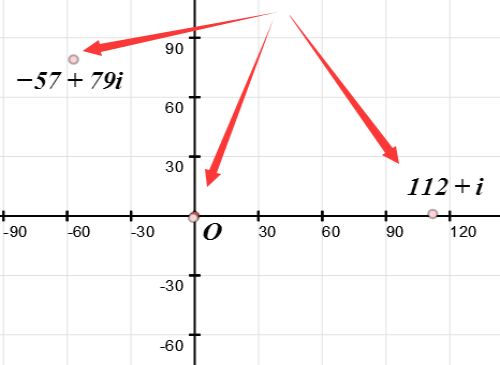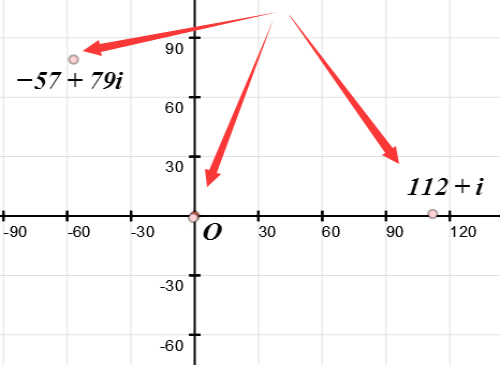

最大公约数的概念。
注意,在某些代数整数环里面,最大公约数未必存在。
但是,Gauss整数环里面肯定存在,因为Gauss整数环是主理想整环。
 2/5
2/5在《【抽象代数】Gauss整数环里面的算术》里面最后,我们给出了两个复数a=7+5i,b=18+5i之间的带余除法。这说明b不能被a整除。
下面,我们要计算b和a的最大公约数,根据Eculid方法,有下式成立。
(18+5i,7+5i)=(-1+2i,7+5i)
 3/5
3/5注意到-1+2i的模长比7+5i小,所以对7+5i和-1+2i进行带余除法。我们在复平面上画出-1+2i、7+5、(7+5i)/(-1+2i),并找出距离(7+5i)/(-1+2i)最近的Gauss整数1-4i。
 4/5
4/5于是有进一步的Eculid方法。
18+5i与7+5i的最大公约数是-i,其实也可以理解为i、1、-1,这四个元素是相伴的。
于是,可以认定,18+5i与7+5i是互素的。
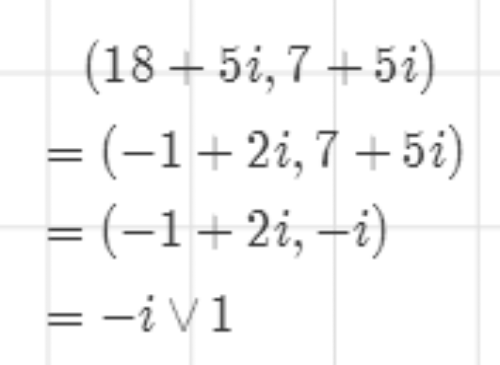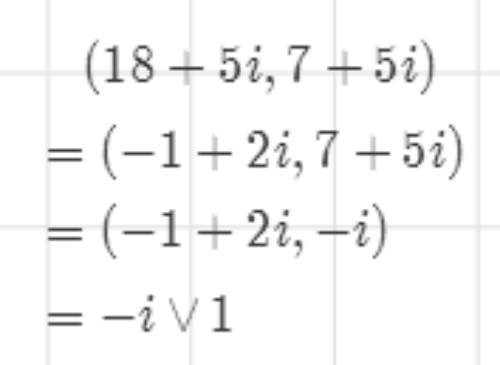 5/5
5/5再举一个例子,a=112+i,b=-57+79i。
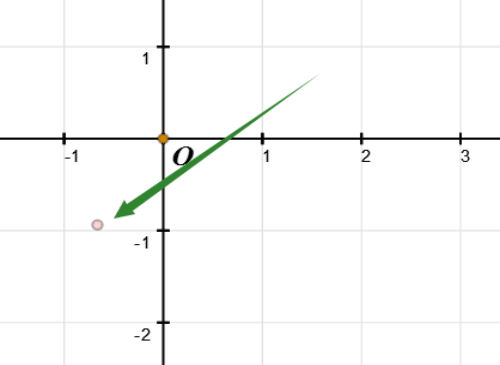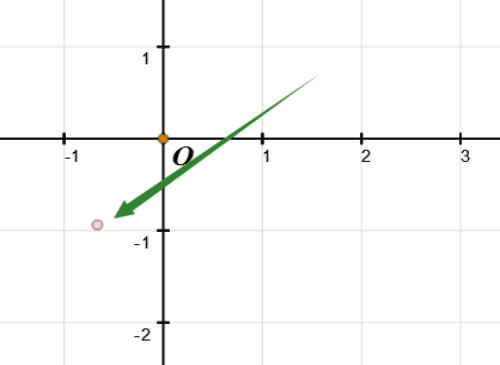
最接近a/b的Gauss整数是-1-i。
112+i-(-1-i)(-57+79i)=-24+23i。



版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_5657.html
上一篇:如何自制冷盘凉拌菜白萝卜
下一篇:如何让桃树果实膨大
 订阅
订阅