【抽象代数】Mathematica怎么输出三对角矩阵?
来源:网络收集 点击: 时间:2024-04-22【导读】:
本文,用Mathematica构造一种最基本的三对角矩阵:三条对角线上的元素都等于1,其余元素都等于0。具体形状如下,这是一个9阶三对角矩阵。工具/原料more电脑Mathematica方法/步骤1/8分步阅读 2/8
2/8 3/8
3/8 4/8
4/8 5/8
5/8 6/8
6/8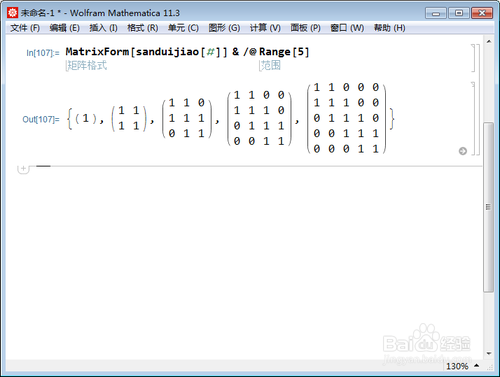 7/8
7/8 8/8
8/8
先给出一个9阶单位矩阵:
A = IdentityMatrix;
 2/8
2/8把第一行的第二个元素置为1,
把第二行的第三个元素置为1,
……
以此类推,直到把第八行的第九个置为1。
这个过程,可以用Mathematica直接表示为:
(A] = 1) /@ Range;
最后一行(第九行)不作处理。
 3/8
3/8对每一列作类似的处理:
(A] = 1) /@ Range;
最后一列不作处理,这样就得到了九阶三对角矩阵。
 4/8
4/8打包成自定义函数,给出其它阶的三对角矩阵:
sanduijiao := Module;
(A] = 1) /@ Range;
(A] = 1) /@ Range;
A]
这个函数返回一个n阶三对角矩阵,前提是,n必须为具体的正整数。
 5/8
5/8测试一下:
MatrixForm]
 6/8
6/8MatrixForm] /@ Range
返回前五个三对角矩阵。
 7/8
7/8n必须为给定的具体正整数,对于未知数,运行会报错:
 8/8
8/8作为一个简单的应用,考察一下不同的三对角矩阵的行列式:
Det] /@ Range
可以发现,随着阶数的逐步增加,三对角矩阵的行列式呈现【周期性】,这个周期为6。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_569528.html
上一篇:好妈妈的标准
下一篇:iPhone 14如何开启电池数字
 订阅
订阅