有5种方法，如下：

（1）利用洛必达法则与等价无穷小代换对抽象函数的00型极限可得结论：设当x→x0时f（x）与g（x）为无穷小,g（x）～（x-x0）β,取k为正实数,使得fk（x）=A（x-x0）α＋o。

其中A〉0,α≥2,β〉0为实数,则有limx→x0f（x）g（x）=1.该方法对求常见的00型极限都适用.当使用洛必达法则求li mx→x0f（x）g（x）很复杂时,使用该方法可简化计算.

（2）因式分解法，约去零因式，从而把未定式转化为普通的极限问题。

（3）如果分子分母不是整式，而且带根号，就用根式有理化的方法，约去零因子。

（4）考虑应用重要极限的结论，从而把问题转化，可以很容易求解。

（5）如果满足等价无穷小代换条件，那么就可以用代换无穷小的方法求解。

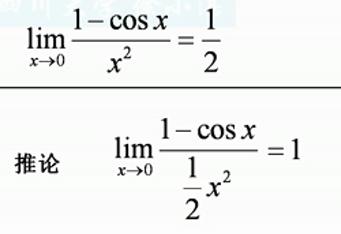
扩展资料：

极限的思想方法贯穿于数学分析课程的始终。可以说数学分析中的几乎所有的概念都离不开极限。在几乎所有的数学分析著作中，

都是先介绍函数理论和极限的思想方法，然后利用极限的思想方法给出连续函数、导数、定积分、级数的敛散性、多元函数的偏导数，广义积分的敛散性、重积分和曲线积分与曲面积分的概念。如：

（1）函数在 点连续的定义，是当自变量的增量趋于零时，函数值的增量趋于零的极限。

（2）函数在 点导数的定义，是函数值的增量 与自变量的增量 之比 ，当 时的极限。

（3）函数在 点上的定积分的定义，是当分割的细度趋于零时，积分和式的极限。

（4）数项级数的敛散性是用部分和数列 的极限来定义的。

（5）广义积分是定积分其中 为，任意大于 的实数当 时的极限，等等。

运算法则：设，存在，且令，则有以下运算法则：

加减：

数乘：

（其中c是一个常数）

乘除：

( 其中B≠0 )

幂运算：

参考资料：极限（数学术语）_百度百科