订阅函数y=log3(3x^2+2)的图像
来源：网络收集 点击： 时间：2024-01-25函数y=log3(3x^2+2)的定义域，结合对数函数的性质，求解函数y=log3(3x^2+2)的定义域。
2/10简单来讲，对于两个变量x和y，如果每给定x的一个值，y都有唯一一个确定的值与其对应，那么我们就说y是x的函数。其中，x叫做自变量，y叫做因变量。
3/10计算出函数y=log3(3x^2+2)的一阶导数，通过函数的一阶导数，求出函数y=log3(3x^2+2)的单调区间。
4/10在函数y=f的定义域内，令μ=g(x)，则y=f的单调性由μ=g(x)与y=f(μ)的单调性共同确定，可用同增异减来判定。
5/10函数的奇偶性，判断函数的奇偶性，由于函数f(-x)=f(x),即函数y=log3(3x^2+2)为偶函数，确定其对称性为关于y轴对称。
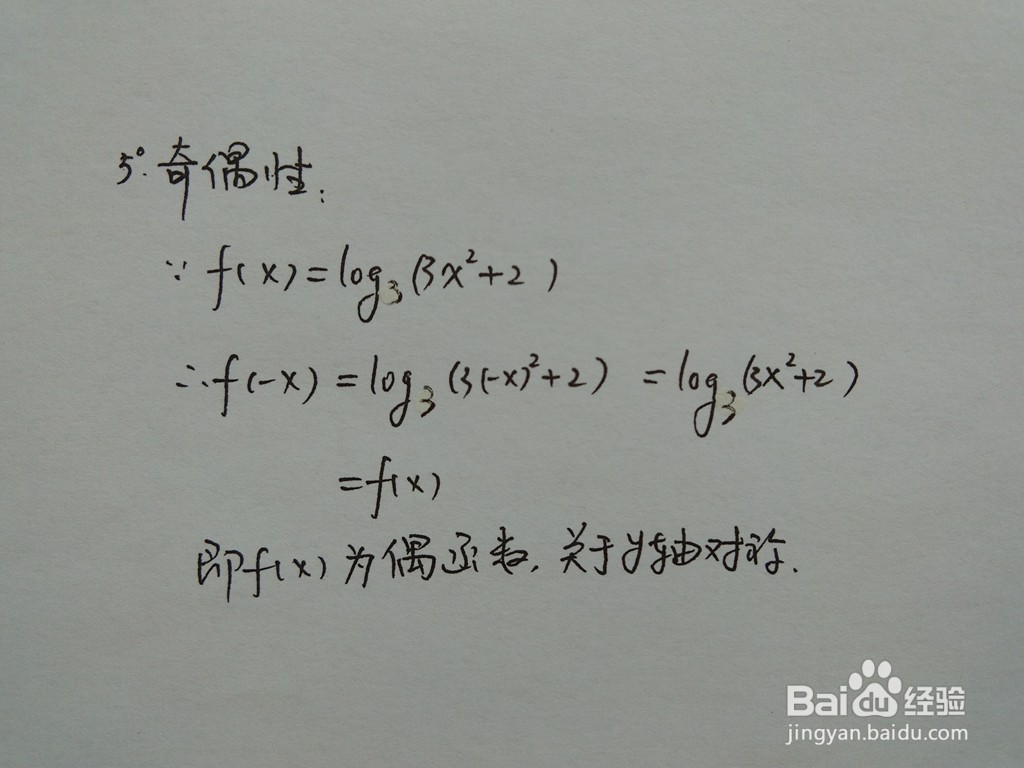6/10函数的奇偶性，设f(x)为一实变量实值函数，则f为偶函数若下列的方程对所有实数x都成立：f(x) = f( - x) 。几何上，一个偶函数会对y轴对称，亦即其图在对y轴为镜射后不会改变。
7/10函数y=log3(3x^2+2)的凸凹性，通过函数的二阶导数，解析函数y=log3(3x^2+2)的凸凹区间。
8/10二阶导数，是原函数导数的导数，将原函数进行二次求导。一般的，函数y=f(x)的导数y=f(x)仍然是x的函数，则y=f(x)的导数叫作函数y=f(x)的二阶导数。
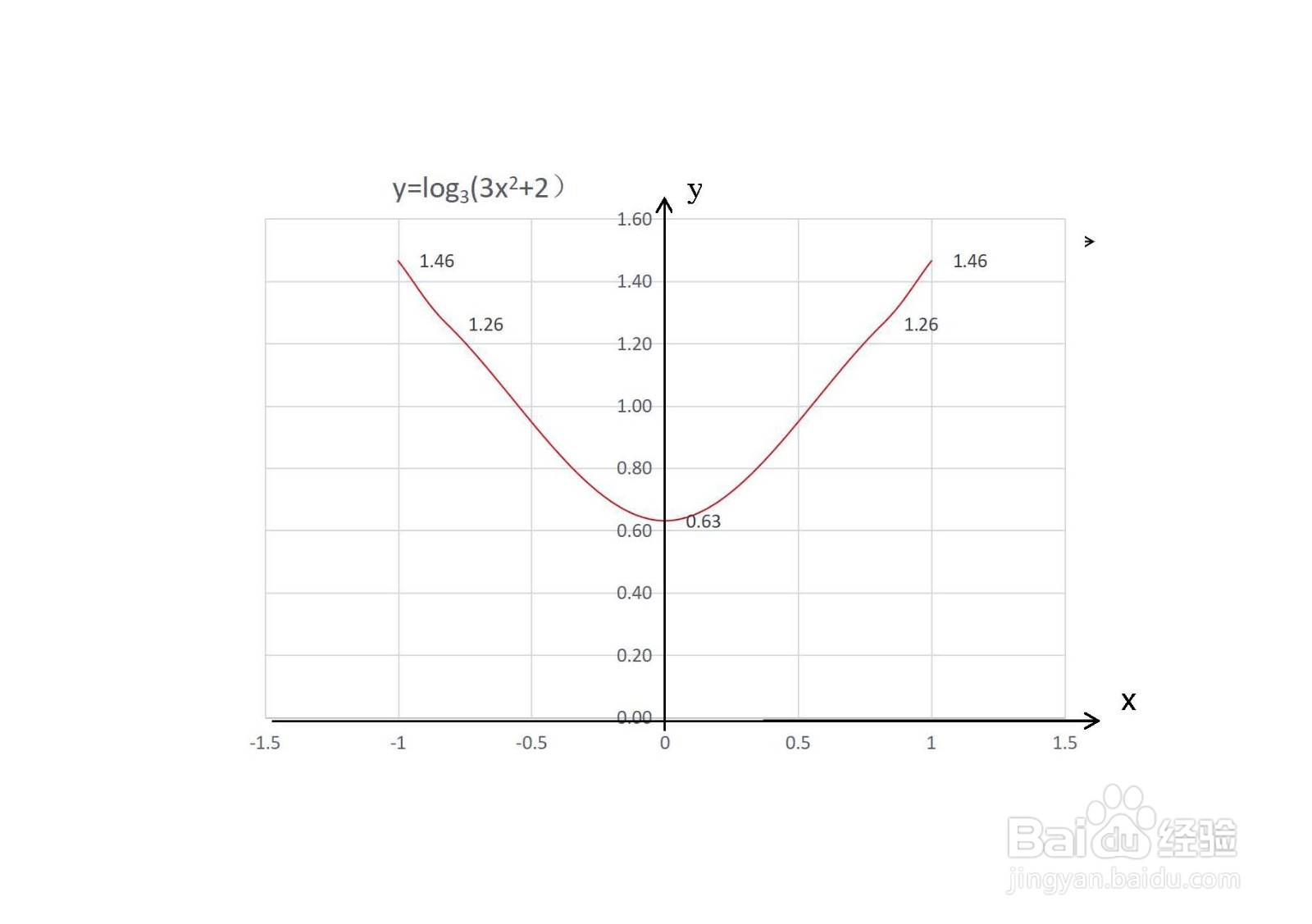
9/10函数y=log3(3x^2+2)图上，部分点以图表解析表列举如下：
10/10综合以上函数的定义域、单调性、凸凹性性、奇偶性和极限等性质，并结合函数的单调区间、凸凹区间，可画出函数y=log3(3x^2+2)的示意图如下：
注意事项一阶导数函数单调性
二阶导数判断函数的凸凹性
图像导数单调性凸凹版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_6387.html
