用微积分知识画函数y=x^3-6x^2+1的图像
来源:网络收集 点击: 时间:2024-05-01【导读】:
本经验通过函数的定义域、单调性、凸凹性、极限等性质,介绍函数用导数工具画函数y=x^3-6x^2+1的图像的主要步骤。工具/原料more导数相关知识主要方法与步骤 1/8分步阅读 2/8
2/8 4/8
4/8 6/8
6/8 7/8
7/8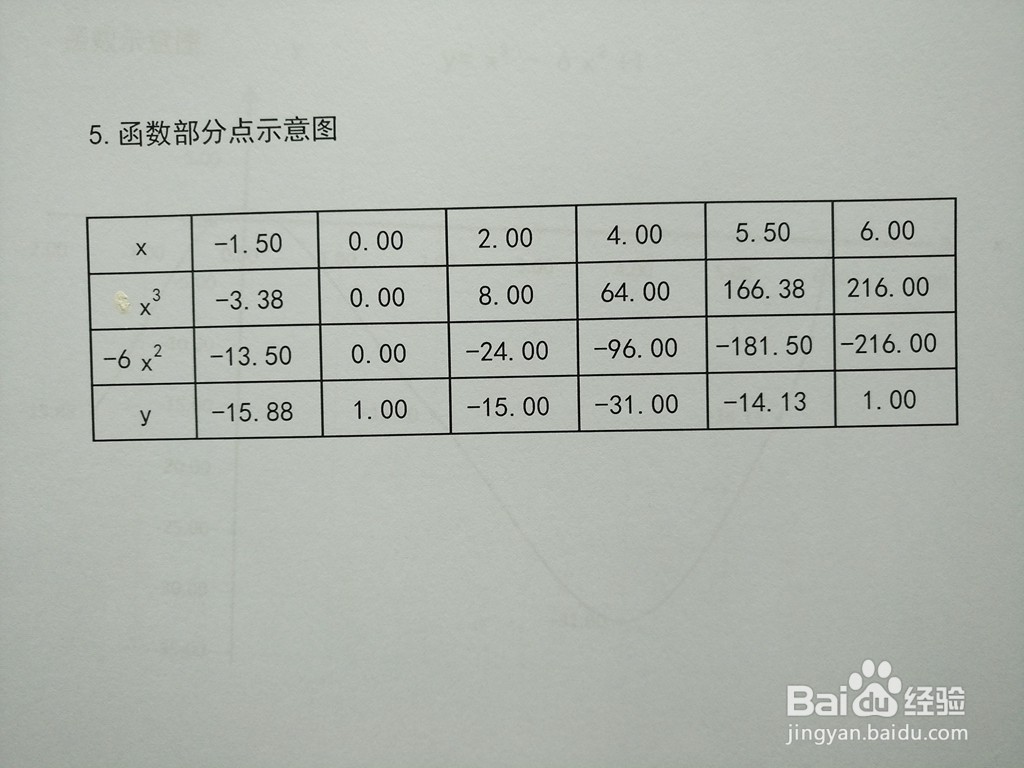 8/8
8/8 注意事项
注意事项
函数的定义域,函数自变量可以取全体实数,即定义域为:(-∞,+∞)。
 2/8
2/8形如y=f(x),则x是自变量,自变量的取值范围就是函数的定义域。f是对应法则的代表,它可以由f(x)的解析式决定。
3/8通过函数的一阶导数,求出函数驻点,判断函数一阶导数的正负,解析函数的单调性,进而得到函数的单调区间。
 4/8
4/8函数的单调性也叫函数的增减性。当函数f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。
5/8通过函数的二阶导数,得函数的拐点,解析函数的凸凹区间。
 6/8
6/8分析函数在正负无穷大处的极限。
 7/8
7/8结合函数的定义域及单调和凸凹性质,函数上部分点解析如下表所示,横坐标和纵坐标。
 8/8
8/8根据函数的定义域、值域、单调性、凸凹性和极限等性质,以及根据函数的单调区间和凸凹区间,则函数的图像示意图如下:
 注意事项
注意事项一阶导数可判断函数的单调性
函数导数单调性凸凹性版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_639303.html
 订阅
订阅