椭圆规，是绘制椭圆的一个非常好用的工具，是人类智慧的结晶，是一个连杆系统。 椭圆规看着构造简单，但是，想要在几何画板里面画出椭圆规，并且生成连续动画，可不是一件容易的事！比如，下面的步骤一，就给出了一个错误的例子。 本文的目的，是要用几何画板来构造一个合理的椭圆规。工具/原料more电脑几何画板方法/步骤1/6分步阅读

这是一个失败的案例：

先画两条互相垂直的直线，以及定长线段AB；

在竖线上画动点D；

以D为圆心、AB为半径作圆，与横线交于C；

连结线段DC；

取DC上一个点M，使DM：MC为定值；

那么，理论上讲，当点D在竖线上移动的时候，M的轨迹就是一个椭圆。然而，事实上，M的轨迹仅仅是半个椭圆，而D正在跑向无穷远的地方，线段DC早就消失了！

2/6

由上图可知，当M是线段DC的中点的时候，M的轨迹应该是圆（事实上是俩半圆）。

于是，我们有了一个可行的方案：我们选择单位圆上任意点M，要求作线段CD，使C在x轴上、D在y轴上、M是CD中点。这样构成的线段CD是不是就完美了呢？

3/6

把上面的问题转化一下：

两射线夹角内有一个点M，过M作线段与两射线交于C、D，且CM：MD=1：1。注意：两射线夹角未必是直角。

作图步骤如下：

延长FM至E，使得FE=2FM；

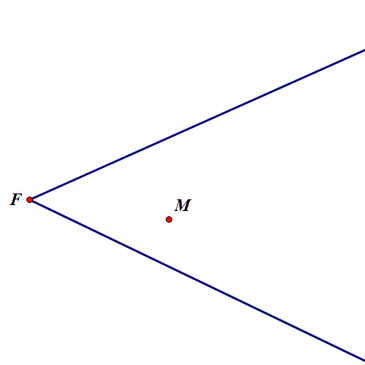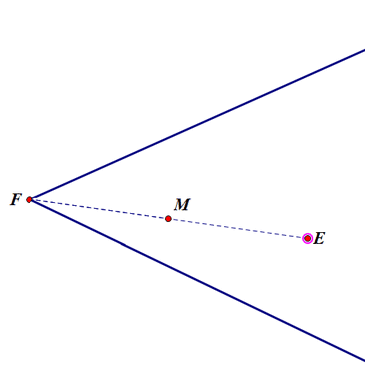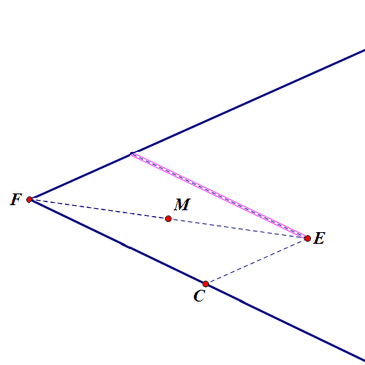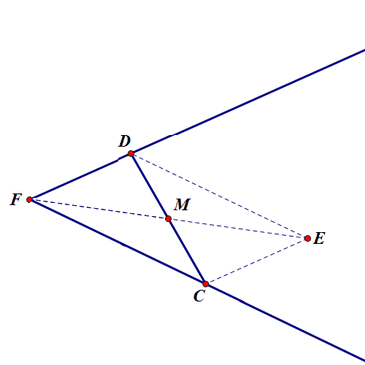
过E作两射线的平行线，各自与另一条射线交于C、D；

连结CD，那么，M就是CD的中点。

4/6

回到椭圆规的问题上：

构造单位圆和过圆心的两条互相垂直的直线；

选择单位圆上的动点M，过M作线段与上面两条互相垂直的直线交于C、D，且CM：MD=1：1；

取线段CD（或直线CD）上任意点N；

选择M和N，点击菜单“构造”——“轨迹”，那么N的轨迹就是椭圆。

这其实给出了一种椭圆的作图方法。

5/6

先前说过椭圆规是连杆系统，那么，我们就把上图补充一下，使之看起来是真正的连杆系统：

设圆心为O，连结OM，可以发现，O和M都是转轴，C和D是固定在两条互相垂直的直线上的滑块。具体的，见下图。

6/6

前面那个问题的推广：

两射线夹角内有一个点M，过M作线段与两射线交于C、D，且CM：MD=AX：XB，其中，ABX是事先给定的。

这个问题，留给读者去思考吧！

注意事项

椭圆规是一个连杆系统。

用几何画板构造椭圆规和连杆系统，都不容易，要费一番功夫。

给读者留一个问题：两射线夹角内有一个点M，过M作线段与两射线交于C、D，且CM：MD=AX：XB，其中，ABX是事先给定的线段。