曲面的柱坐标与球坐标方程及在三重积分中的应用
来源:网络收集 点击: 时间:2024-05-19【导读】:
在利用柱坐标系和球坐标系计算三重积分时,为求出积分限,通常须要把积分区域Ω的边界曲面方程转化为柱坐标或球坐标的形式,为此本节对这两种坐标系作进一步介绍,并以圆锥面和旋转抛物面为例说明曲面柱坐标与球坐标方程的求法,最后总结常见曲面的在三种坐标系下的方程,并以此说明计算三重积分时如何选取坐标系。本系列文章上一篇见下面的经验引用:工具/原料more高等数学基础知识方法/步骤1/6分步阅读 2/6
2/6 3/6
3/6 4/6
4/6 5/6
5/6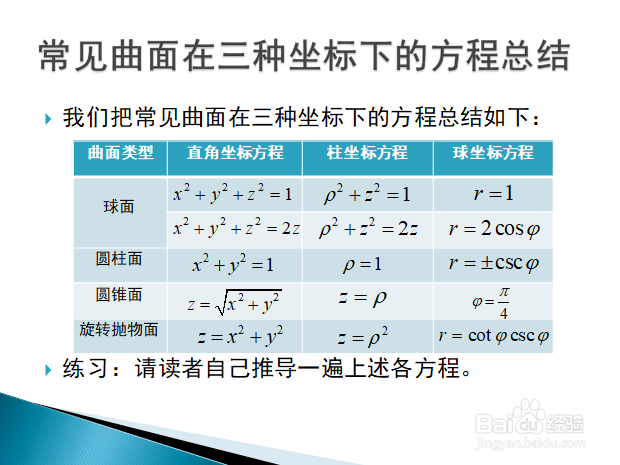 6/6
6/6 注意事项
注意事项
概述(柱坐标变换与球坐标变换复习)。
 2/6
2/6柱坐标系与球坐标系中的坐标面。(在这两种坐标系中,某个坐标为常数时表示怎样的曲面?)
 3/6
3/6圆锥面的柱坐标与球坐标方程的求法。
 4/6
4/6旋转抛物面的柱坐标与球坐标方程的求法。
 5/6
5/6常见曲面在三种坐标系下的方程总结(请读者练习自己推导)。
 6/6
6/6在计算三重积分时,如何根据积分区域Ω的特点选择合适的坐标系?
 注意事项
注意事项感谢您的浏览,如果本经验对您有所帮助,欢迎您投票、转发、收藏和评论。
欢迎您继续阅读本系列的后续文章,后续文章更新后可在本人的经验首页找到。
高等数学大学数学考研数学理工学科版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_803299.html
上一篇:青菜绿豆汤的做法
下一篇:手机软件soul 如何帮好友捏脸?
 订阅
订阅