Mathematica应用——绘制精美的3D图形
来源:网络收集 点击: 时间:2024-05-19【导读】:
Mathematica可以作出很多复杂的方程的曲线和曲面。下面,我们就来看看在三维空间里面的一些比较容易写出代数方程的曲面!工具/原料more电脑Mathematica方法/步骤1/6分步阅读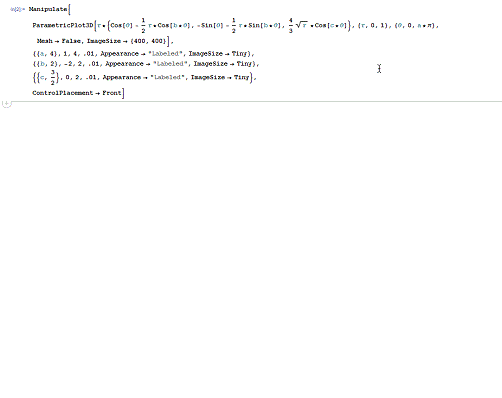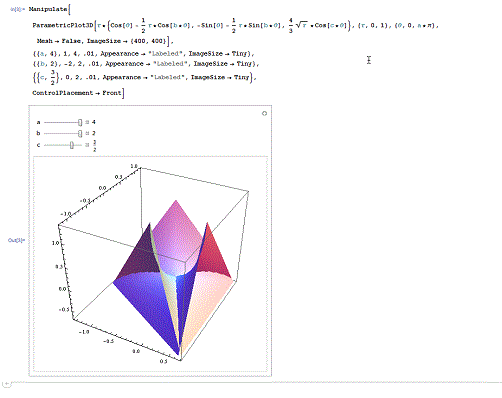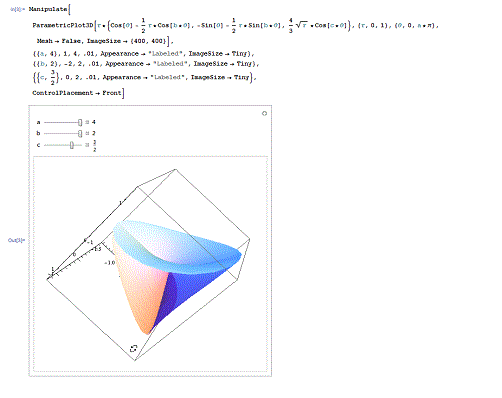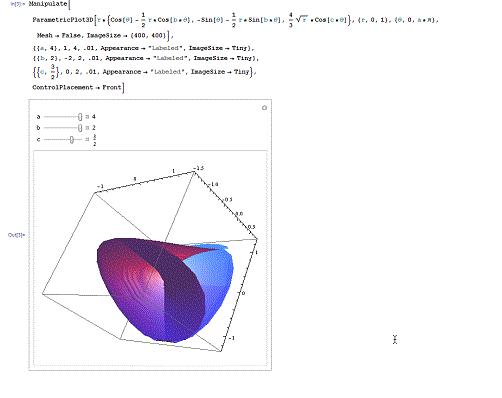 2/6
2/6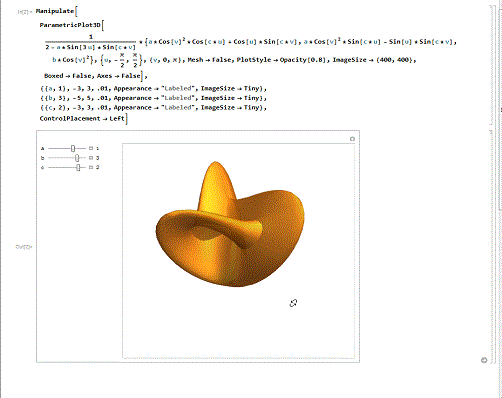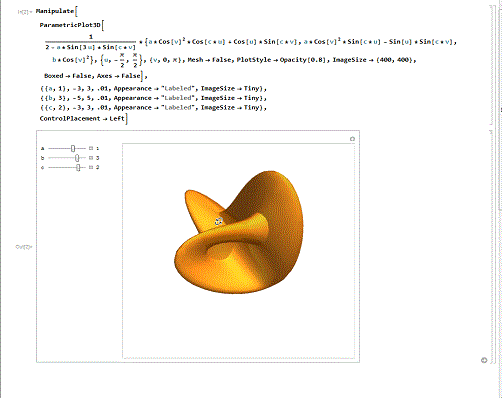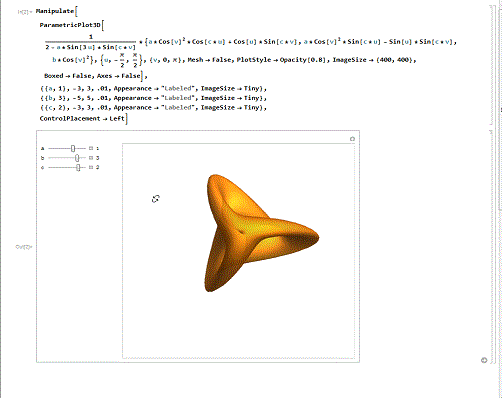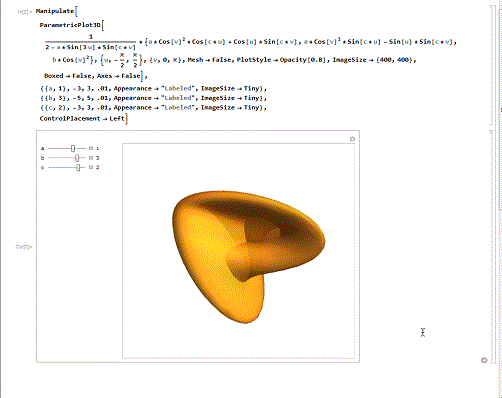 3/6
3/6
 4/6
4/6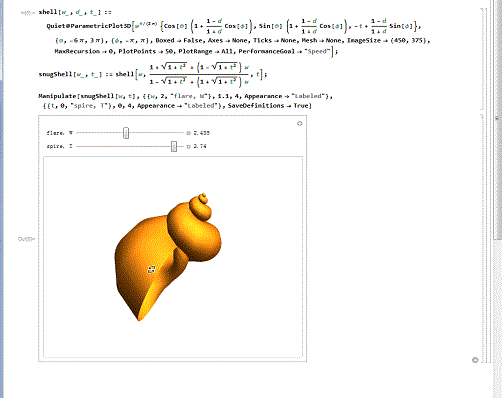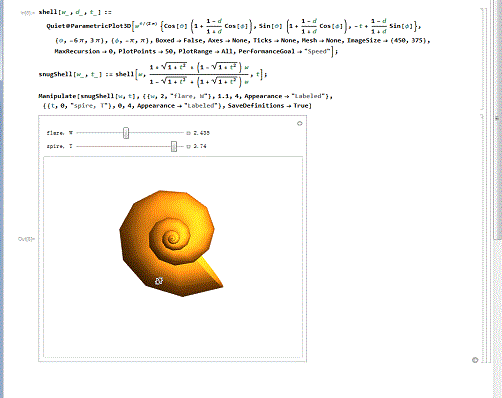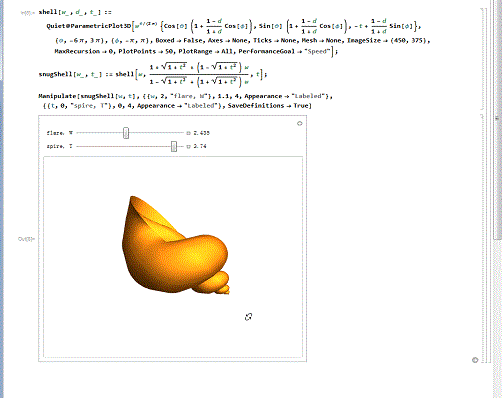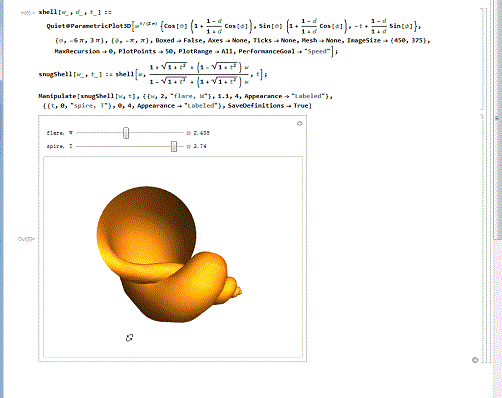
 5/6
5/6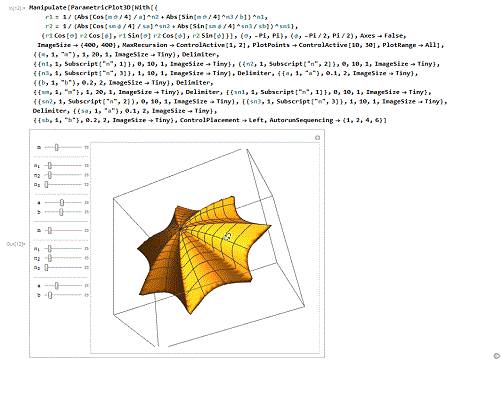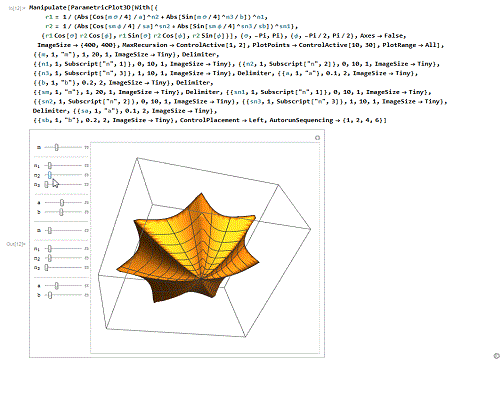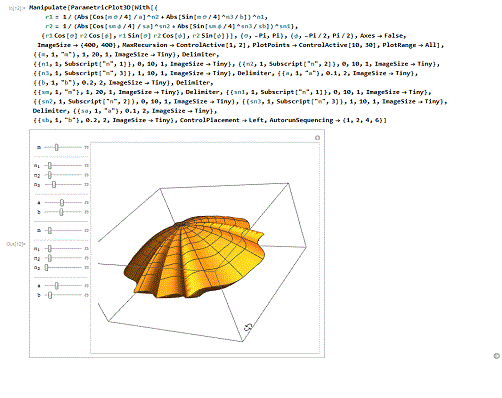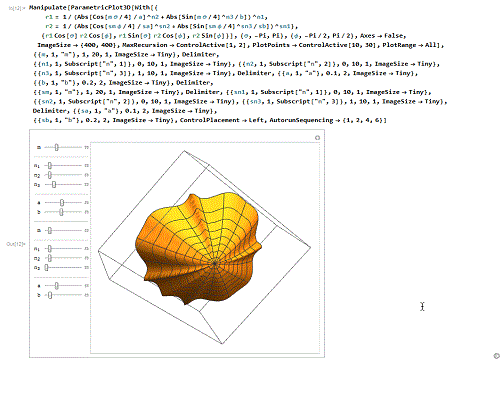 6/6
6/6 注意事项
注意事项
第一个,Bour极小曲面。
下面代码演示了Bour极小曲面在a=4、b=2、c=3/2时的情形,并展示了其他情形的变化。
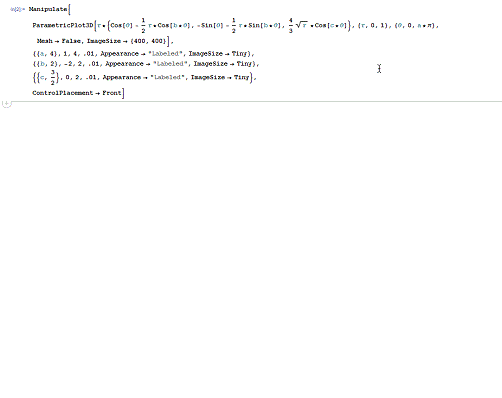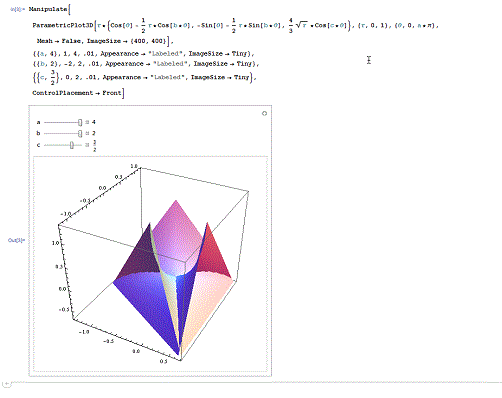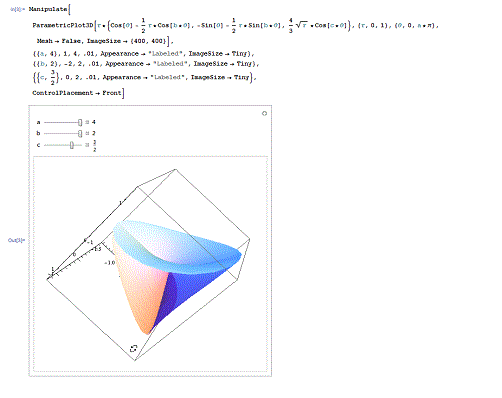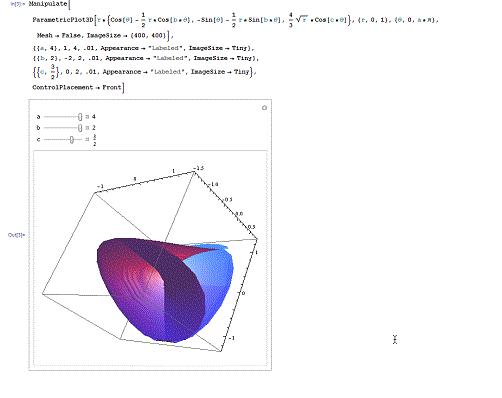 2/6
2/6第二个,Boy曲面。
Boy曲面的表面是一个不可定向曲面,你可以顺利的在内表面上跑到外表面上。改变参数a、b、c的取值,可以观察到不一样的情景!
 3/6
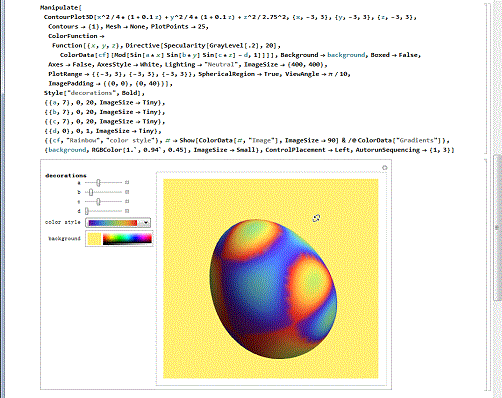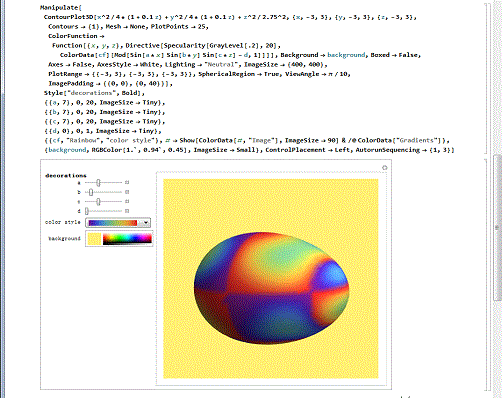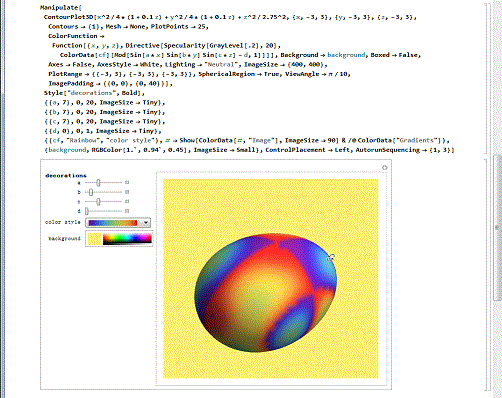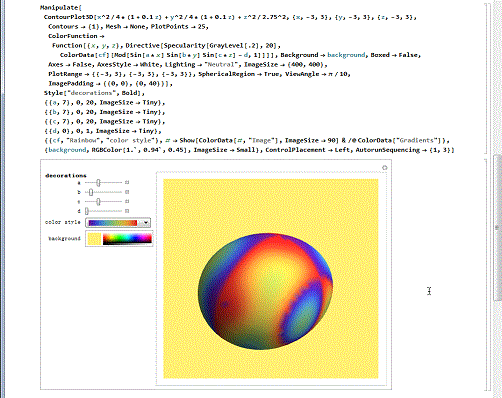
3/6彩色的蛋壳。
用参数和不同的着色手段,可以绘制出精美的彩色蛋壳,真是好看!
第一个蛋壳的着色方法是Gradients——渐变;第二个蛋壳使用的是Sinusoids着色法(窦状着色法)。
还可以用其他的着色方法,比如:斑马色(ZebraColor)、多项式着色(Colored Using Polynomials)、黎曼函数着色(Colored Using the Riemann Zeta Function)、球极坐标着色(Spherical Coordinates)……

 4/6
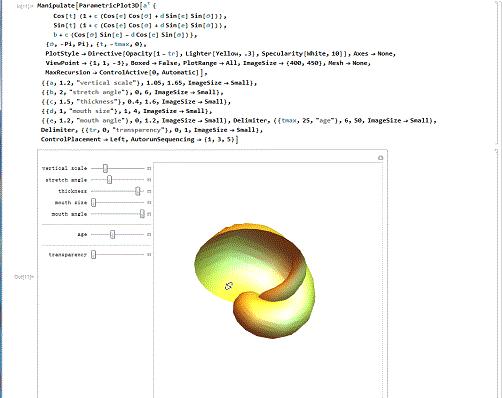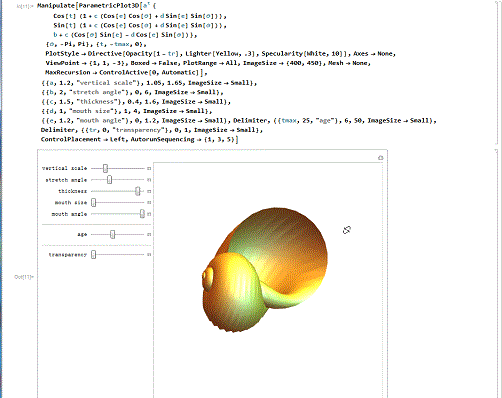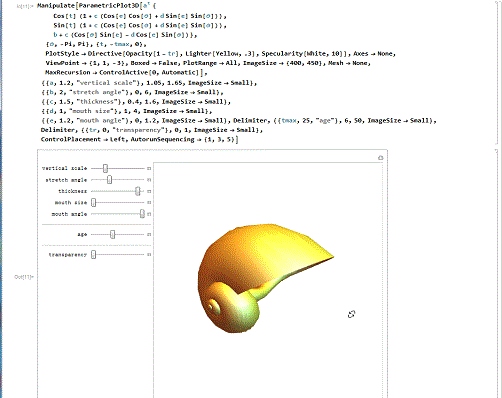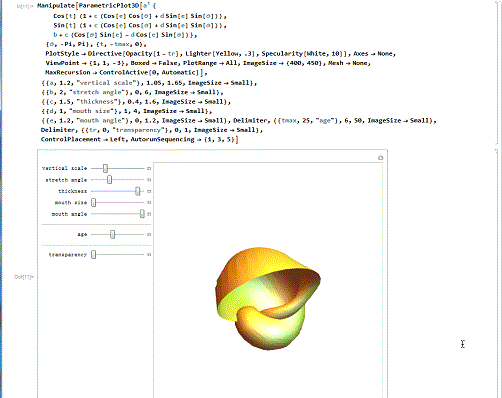
4/6漂亮的贝壳。下面的代码,绘制了某种精美的贝壳曲面,还能演示贝壳的生长过程!

 5/6
5/6超椭球曲面。
这个就要涉及到超椭球函数,不解释,只欣赏!
 6/6
6/6类似于球极函数的图像,但其实是采用复变函数的方法绘制的!
 注意事项
注意事项三维曲面的内容很丰富,欲学习相关内容,请先自学射影几何、微分几何和曲面论!
MATHEMATICA曲面版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_806055.html
上一篇:天天的朋友站在他爸爸身边怎么改
下一篇:狗狗产后吃什么恢复快
 订阅
订阅