网络画板又有新能力了，可以画轨迹曲线的交点了。这已经超越了几何画板了。 下面，我就用这一点，来处理等内切圆问题：在△ABC所在平面上找到点D，使得△ABD、△BCD、△CAD的内切圆半径相等。 事先说明，我用的方法不属于“尺规作图”，而是交轨法。工具/原料more电脑互联网+浏览器网络画板方法/步骤1/10分步阅读

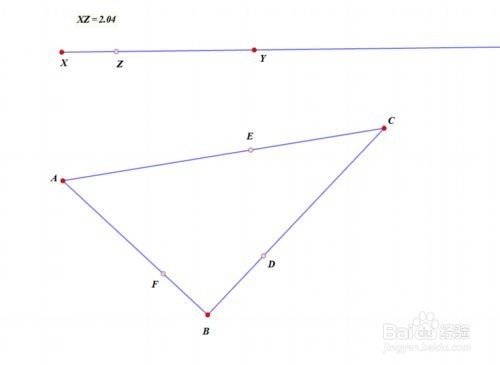
先绘制△ABC，要求A、B、C是平面上的自由点，这样，可以保持作图的一般性，便于手动操作和观察；

D、E、F分别是线段BC、CA、AB上的半自由点。

2/10

绘制射线XY以及射线上的半自由点Z，测量X、Z之间的距离。

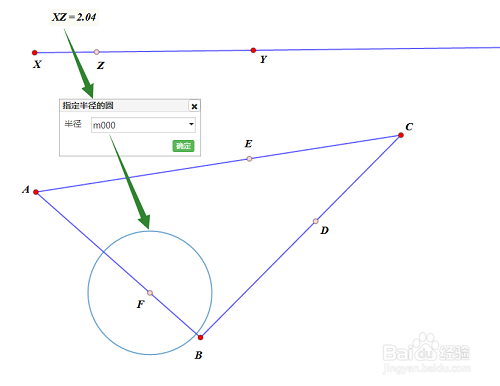
3/10

以F为圆心、XZ为半径作圆F；过F作AB的垂线，与圆F交于F，且F和点C位于AB同侧；作圆F—F。这里，之所以限定F和点C位于AB同侧，是为了防止画板卡掉，尽量减少几何图形。

同样地，对D、E两点，执行类似的操作。

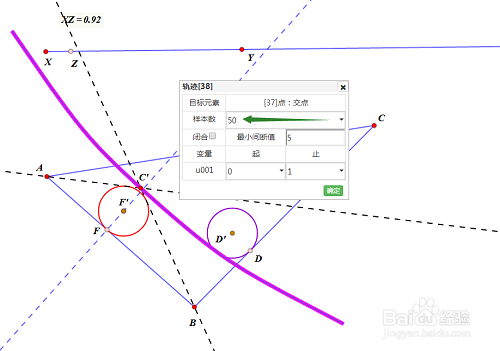
4/10

分别过A、B，作圆F的异于直线AB的切线，这两条切线交于C；

先后选择F、C，构造轨迹（图中红色的曲线，样本数改为50）；

所以，这条轨迹上的任一点与AB围成的三角形的内切圆半径都是XZ。

5/10

拖动Z，这条红色曲线发生改变，这是因为对应的内切圆半径发生变化。

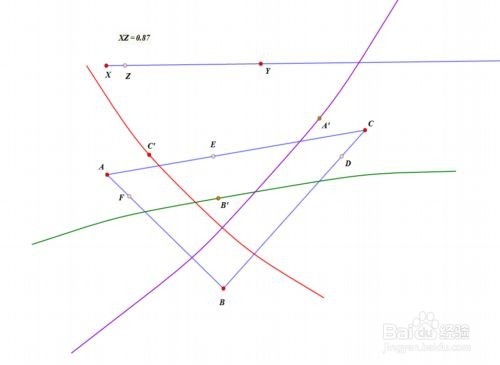
6/10

类似于步骤4：

分别过B、C，作圆D的异于直线BC的切线，这两条切线交于A；先后选择D、A，构造轨迹（图中紫色的曲线，样本数改为50）；

分别过A、C，作圆E的异于直线AC的切线，这两条切线交于B；先后选择E、B，构造轨迹（图中绿色的曲线，样本数改为50）。

拖动点Z，看看什么效果！

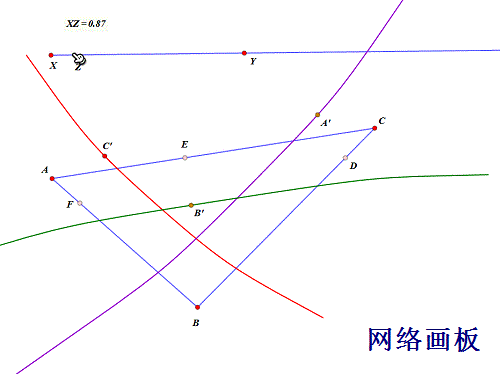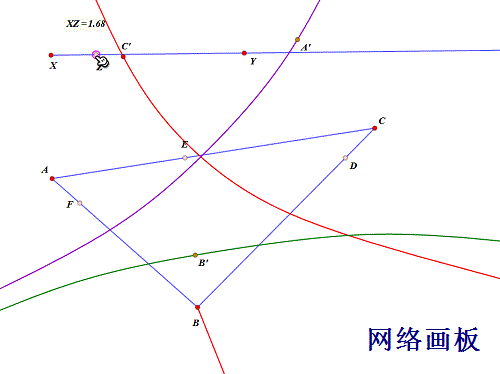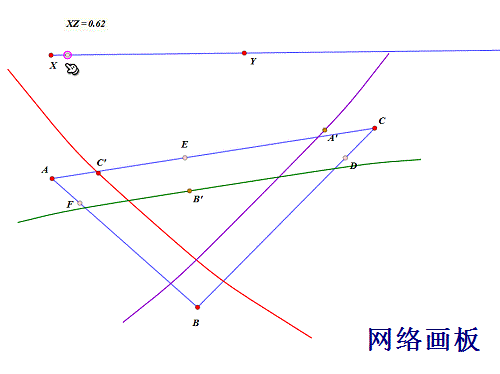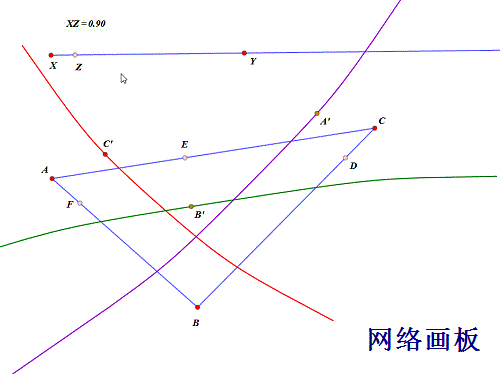7/10

设三条轨迹曲线分别交于P、Q、R，此时必有：

△PBA和△PBC的内切圆半径相等；

△QCA和△QCB的内切圆半径相等；

△RAB和△RAC的内切圆半径相等。

当P、Q、R重合的时候，就达到了我们一开始的目标。

8/10

先后选择Z、P，构造轨迹（可能有点卡，把样本数改为50就会好一点，图中的绿色粗线）；

先后选择Z、Q，构造轨迹（可能有点卡，把样本数改为50就会好一点，图中的红色粗线）；

P和Q的轨迹线的交点，就是要作的D点。

这里，可以肯定的是，R的轨迹也过D，所以，为了防止画板变得更卡，就不画R的轨迹线了。

9/10

验证一下：

先隐藏多余的几何图形；

构造△ABD、△BCD、△CAD的内切圆，分别测量它们的半径，然后拖动A、B、C三点，观察数值变化，应该恒等。

理论上是相等的，但是测量可能有误差，大概和样本数过低有关！

10/10

至此，这个问题解决了一半了。

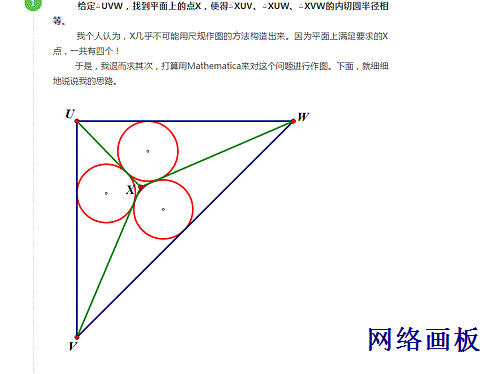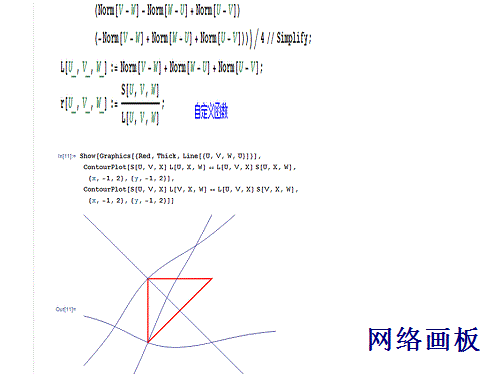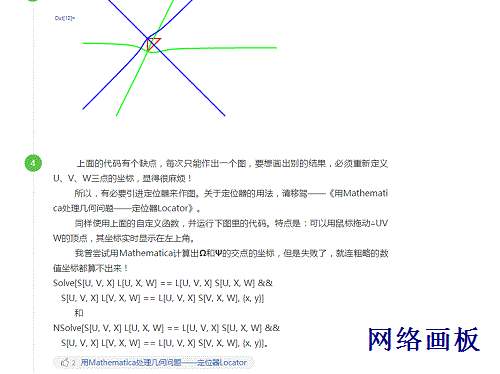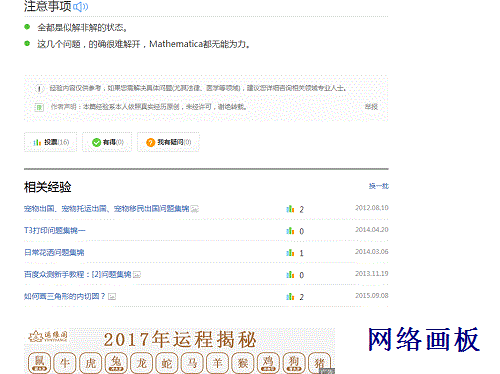
事实上，满足要求的D应该有四个，其中一个位于△ABC内部，就是我们刚才构造的，还有三个位于△ABC外部，在每个角的区域范围内各有一个。具体信息，参考《等内切圆的部分问题集锦》。

由于网络画板构造一个D就已经很卡了，所以，我现在没法作出D的所有的四个解，只能算是完成了一半！

注意事项

D能不能用尺规作图的方法进行构造？

这个例子，反映出网络画板的一个缺陷，就是构造轨迹的时候，很容易卡掉！还有待继续优化！

网络画板实现了轨迹的交点了，又有智能画笔。我估计，几何画板如果不能赶上进度，很快就会被压制下去。

网络画板等内切圆问题