级数收敛的判别方法
来源:网络收集 点击: 时间:2024-05-27【导读】:
我们都知道级数理论在存数学分析里占到很特别的一席之地,而在级数理论里,发现无穷级数的收敛的性则是比较的重要。我们由收敛理论来判段级数的敛散性,然而在实际问题时,通常是不可用的,下面小编来为大家详细介绍一下。工具/原料more细数专业书级数相关的概念方法/步骤1/5分步阅读 2/5
2/5 3/5
3/5 4/5
4/5 5/5
5/5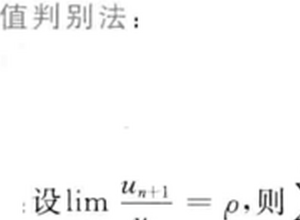 总结1/1
总结1/1
第一步,大家对于全部级数都可以通用的一些主要方法有:柯西收敛准则。那么有关它的本质是把级数来转换成数列,从而这是一个最强的判别法。
 2/5
2/5第二步,接着柯西收敛准则能成立的时候就有可能是级数收敛的中必要条件,然后我们就从数项级数的定里中进入,接着我们来了解和学习数项级数一些的收敛定论。
 3/5
3/5第三步,我们就跟着来挖掘出其中一部分里的数列收敛判别法,然后变为余和判别法,大家一定要熟练掌控项数的特征。
 4/5
4/5第四步,我们接着就可以引导出来夹逼定理与奇、接着就是偶子级数收敛的辨别法、接着就是Cauchy的收敛的准则。
 5/5
5/5我们经常研究项级数的收敛办法:接着就是交错级数里的Leibniz辨别法与Dirichlet辨别法,然后就根据其中的来判定数列是否收敛。
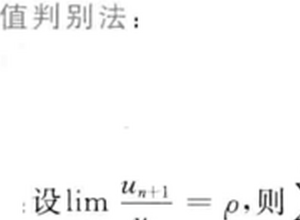 总结1/1
总结1/11.通用的法则有柯西收敛法则。
2.充分了解关于细数收敛定义与掌握。
3.接着就是交错级数里的Leibniz辨别法与Dirichlet辨别法,然后就根据其中的来判定数列是否收敛。
注意事项从来没有一成不变的办法。
熟练运用定义来辨别细数收敛的定义。
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_843343.html
上一篇:传奇服务器被攻击后怎么处理
下一篇:Ae如何成功锁定参考线
 订阅
订阅