线性代数:矩阵相似和对角化?
来源:网络收集 点击: 时间:2024-06-02【导读】:
授人予鱼不如授人予渔,在《线性代数》的学习中,方法尤为重要。下面就让我们一起解决《线性代数》中令人头痛的——矩阵相似和对角化问题吧!如果您对——矩阵相似和对角化的学习比较吃力,建议您先学习——伴随矩阵和逆矩阵,传送门开启,嘛咪嘛咪哄!工具/原料more线性代数课本笔、纸一、矩阵相似的定义和性质1/5分步阅读 2/5
2/5 3/5
3/5 4/5
4/5

 5/5
5/5 二、求对角矩阵例题1/3
二、求对角矩阵例题1/3 2/3
2/3

 3/3
3/3
 三、特征值与对角化的联系1/1
三、特征值与对角化的联系1/1 四、对角化和特征值例题1/2
四、对角化和特征值例题1/2

 2/2
2/2

 五、实对称矩阵的含义1/2
五、实对称矩阵的含义1/2 2/2
2/2


 六、经典例题归纳1/1
六、经典例题归纳1/1

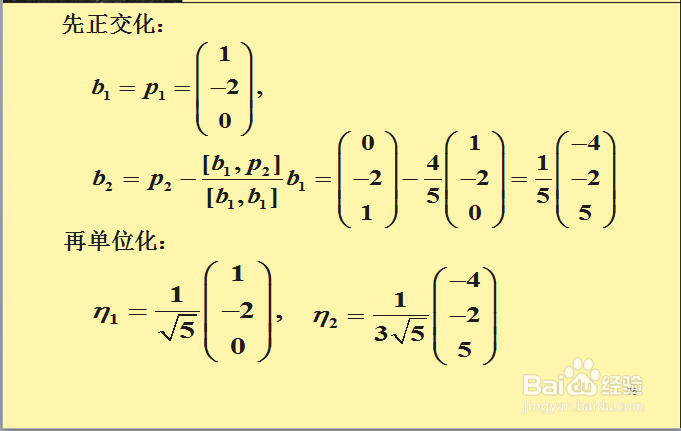

 七、结语1/1
七、结语1/1
矩阵相似定义,如下:
 2/5
2/5矩阵相似关系是一种等价关系:
 3/5
3/5相似矩阵有相同的特征向量和特征值:
 4/5
4/5推论:矩阵A与对角矩阵相似,有以下定理:


 5/5
5/5矩阵相似和对角化的注意点:
 二、求对角矩阵例题1/3
二、求对角矩阵例题1/3判断下列实矩阵能否化为对角阵:
 2/3
2/3题目一,解答如下:


 3/3
3/3题目二,解答如下:

 三、特征值与对角化的联系1/1
三、特征值与对角化的联系1/1定理如下:
 四、对角化和特征值例题1/2
四、对角化和特征值例题1/2例题1、由特征值、特征向量求矩阵:


 2/2
2/2例题2、求方阵的幂:


 五、实对称矩阵的含义1/2
五、实对称矩阵的含义1/2一定可以对角化的矩阵称为实对称矩阵:
 2/2
2/2实对称矩阵的定理与印证:



 六、经典例题归纳1/1
六、经典例题归纳1/1例题如下,注意解答过程:


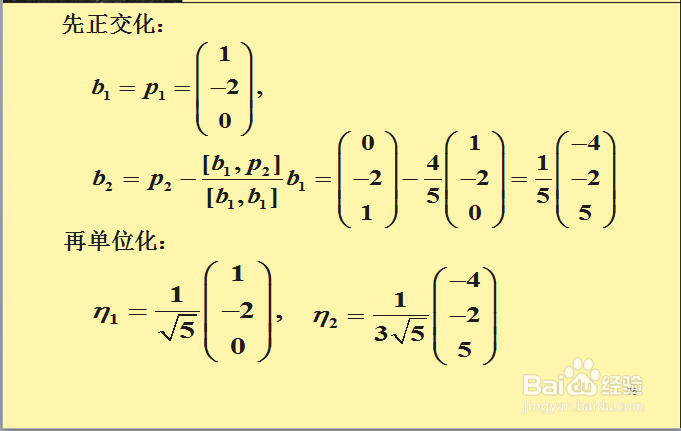

 七、结语1/1
七、结语1/1关于矩阵相似和对角化已经讲解完了,祝贺您今天又学习了新知识。
注意事项今天讲解了矩阵相似,更多精彩内容,敬请关注!
如果您觉得这篇经验有所帮助,别忘了投上您宝贵的一票哦!
代数矩阵相似对角化特征向量特征值版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_872563.html
上一篇:iPhone未解锁时允许访问家庭控制
下一篇:天猫天天特卖限购设置错了怎么办
 订阅
订阅