lnn分之一是发散，因为他小于n分之一，而n分之一发散。

首先可根据级数收敛的必要条件，级数收敛其一般项的极限必为零；反之，一般项的极限不为零级数必不收敛，这样，∑lnn 、∑（lnn分之n）一般项的极限为无穷，必不收敛。

若一般项的极限为零，则可选择某些正项级数审敛法，如比较、比值、根值等审敛法，这样，∑（lnn分之1）可采用比值审敛法，如下(下列都是n趋于无穷)：

lim(1/lnn)/(1/n)=lim(n/lnn)=limn=无穷

又∑ln（1/n）发散，所以 ∑（lnn分之1）发散。

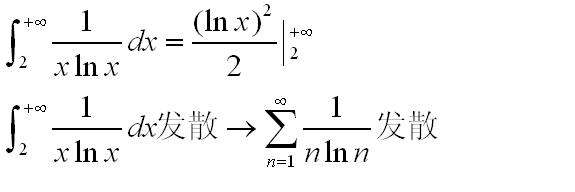
迭代算法的敛散性：

1.全局收敛

对于任意的X0∈，由迭代式Xk+1=φ（Xk）所产生的点列收敛，即其当k→∞时，Xk的极限趋于X*，则称Xk+1=φ（Xk）在上收敛于X*。

2.局部收敛

若存在X*在某邻域R={X| |X-X*|δ}，对任何的X0∈R，由Xk+1=φ（Xk）所产生的点列收敛，则称Xk+1=φ（Xk）在R上收敛于X*。