为什么要进行傅里叶变换？将时域的信号，变换到频域的正弦信号：正弦比原信号更简单，且正弦函数很早就被充分地研究，处理正弦信号，比处理原信号更简单；正弦信号的频率保持性：输入为正弦信号，输出仍是正弦信号，幅度和相位可能发生变化，但频率与原信号保持一致；只有正弦信号才拥有这样的性质工具/原料moreMATLAB傅里叶变换的知识背景介绍1/3分步阅读

第一步：认清并了解傅里叶变换的类型（掌握基本概念）

非周期连续信号：傅里叶变换

周期连续信号：傅里叶级数

非周期离散信号：离散时间傅里叶变换

周期离散信号：离散傅里叶级数

2/3

第二步：从离散傅里叶级数(DFS) 到离散傅里叶变换(DFT)

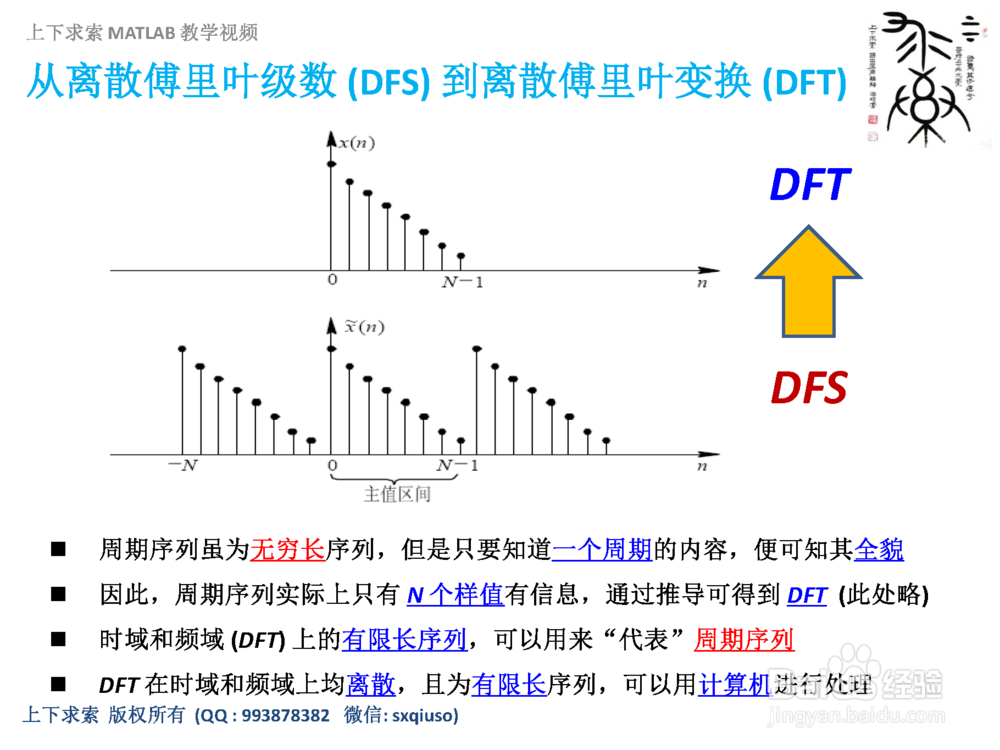
1. 周期序列虽为无穷长序列，但是只要知道一个周期的内容，便可知其全貌

2. 因此，周期序列实际上只有N 个样值有信息，通过推导可得到DFT(此处略)

3. 时域和频域(DFT) 上的有限长序列，可以用来“代表”周期序列

4. DFT在时域和频域上均离散，且为有限长序列，可以用计算机进行处理

3/3

第三步：从离散傅里叶变换(DFT) 到快速傅里叶变换(FFT)

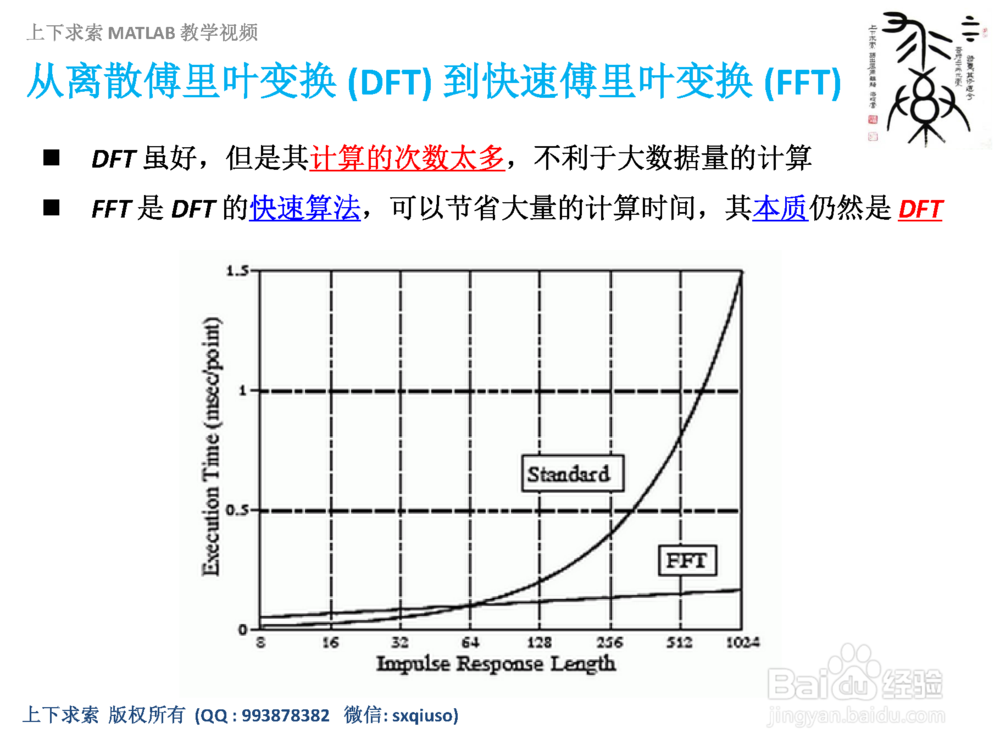
1.DFT 虽好，但是其计算的次数太多，不利于大数据量的计算

2.FFT是DFT 的快速算法，可以节省大量的计算时间，其本质仍然是DFT

3. 此篇经验便是叙述快速傅里叶变换 FFT 在 MATLAB 中的实现方法，以及结果解读

MATLAB 中实现 FFT 的计算1/7

MATLAB 中实现FFT 的计算

Y = fft(x) % x 为一个序列(向量)，存放采集信号的数据

Y = fft(x,n) % x 的定义同上，n 定义计算数据的个数

1. 如果n 大于x 的长度，在x 的末尾添加0，使得x 的长度等于n

2. 如果n 小于x 的长度，截取x 中的前n 个数来进行计算

3. Y 返回fft 的结果，为一个复数序列(向量)

4. 建议：采用第一种格式的用法，并且保证x 的个数为偶数

2/7

频谱应该怎么看：频谱关于中间位置对称 (序号位置0 和N/2 除外) MATLAB 的FFT 为对称谱，看MATLAB 中FFT 的频谱，只需要看一半

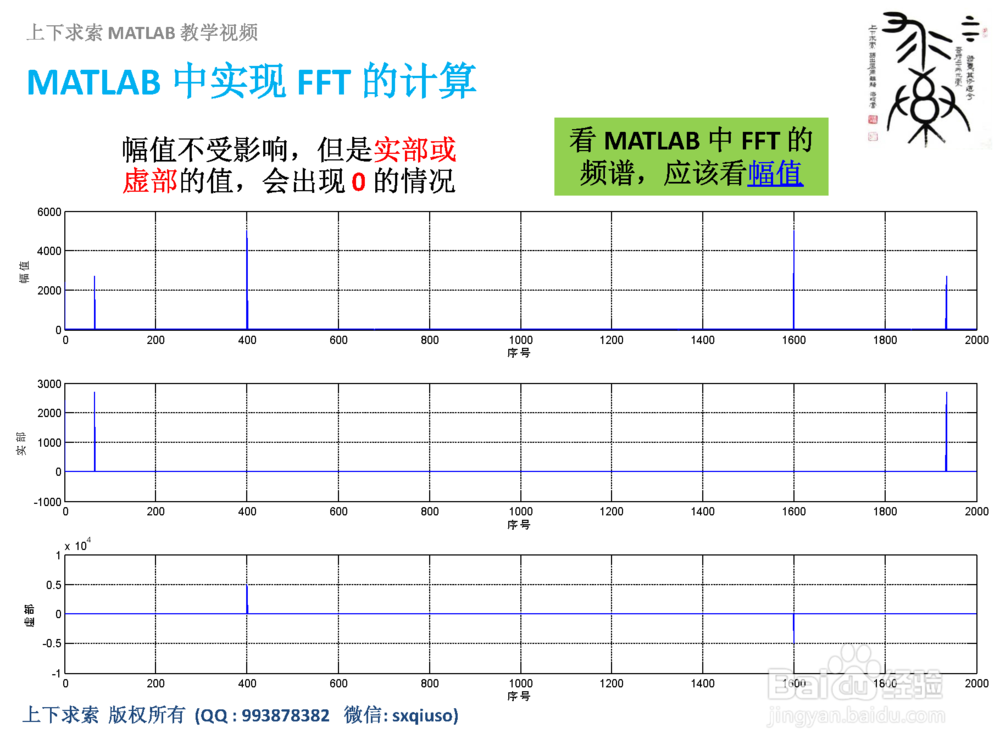
3/7

更改输入信号的设置：将第一个余弦信号的相位改为0，第二个余弦信号的相位改为π/2，观察幅值、实部和虚部的变化。频谱的幅值不受影响，但是实部或虚部的值，会出现 0 的情况，看MATLAB 中FFT 的频谱，应该看幅值

4/7

横轴频率点的设置

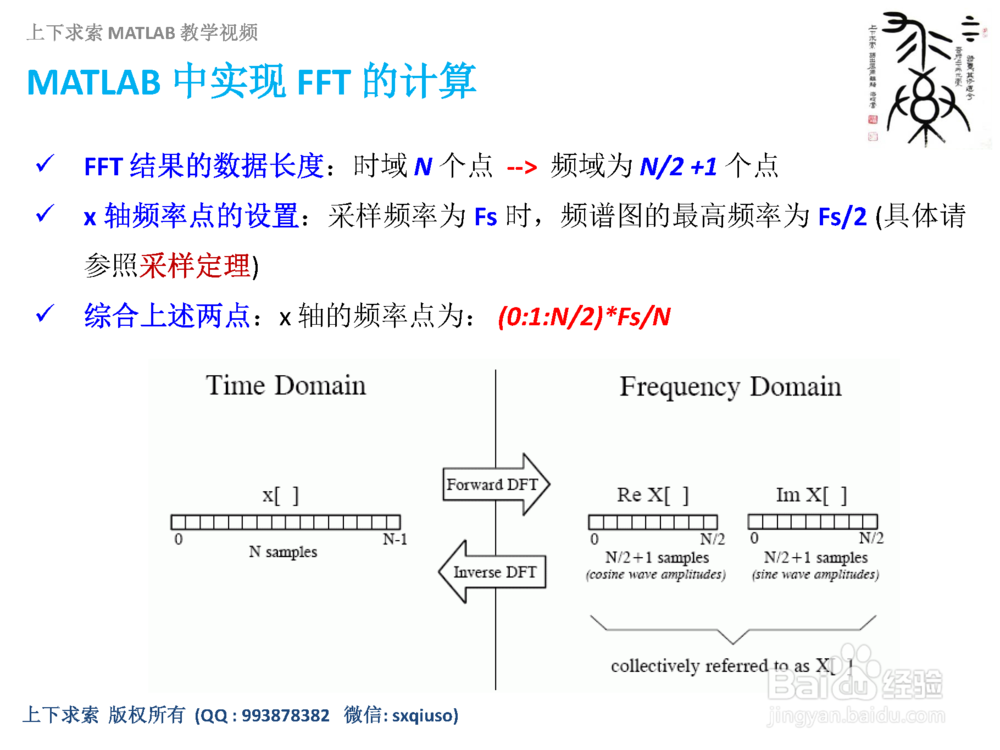
1.FFT结果的数据长度：时域N个点--频域为N/2+1个点

2.x轴频率点的设置：采样频率为Fs时，频谱图的最高频率为Fs/2(具体请参照采样定理)

3.综合上述两点：x轴的频率点为：(0:1:N/2)*Fs/N

5/7

纵轴幅值的修正

MATLAB里fft函数的结果，复数序列Y的幅值，需要进行转换，才能得到与时域中对应信号的幅值

6/7

对信号进行FFT分析，请多多注意傅里叶变换FFT的两个基本问题

7/7

学完了以上的内容，自己来尝试分析一个信号吧~

根据以上所述的方法和步骤，读入一组采集信号，进行傅里叶变换并分析

注意事项

信号处理是基础

MATLAB是工具