卷积运算可以说是一种有别于其他运算的新型运算，在信号处理工作中，它是一种常用的工具。随着信号与系统理论研究的深入以及计算机技术的发展，卷积运算被广泛地运用到诸多新处理领域中，如：现代地震勘测，超声诊断，光学诊断，光学成像，系统辨识及其他。 信号的卷积是针对时域信号处理的一种分析方法，它一般用于求取信号通过某系统后的响应。在信号与系统中，我们通常求取某系统的单位冲激响应，所求得的h(k)可作为系统的时域表征。任意系统的系统响应可用卷积的方法求得：y（k）=x（k）*h（k） 本片经验我们就来说说如何利用matlab来实现两个有限长序列的卷积。工具/原料more配置不错的电脑正常工作的matlab软件原理方法1/3分步阅读

基本数学原理

我们假设有两个长度有限的任意序列A(n)和B(n)，其中A(n)和B(n)的具体数学表达式可以看下图一。那么这两个有限长序列的卷积就应该为C(n)=A(n)*B(n)，其具体表达式请参看一下图二。

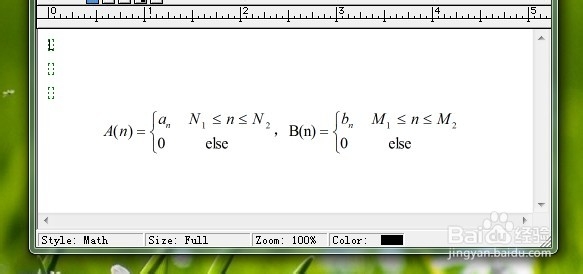
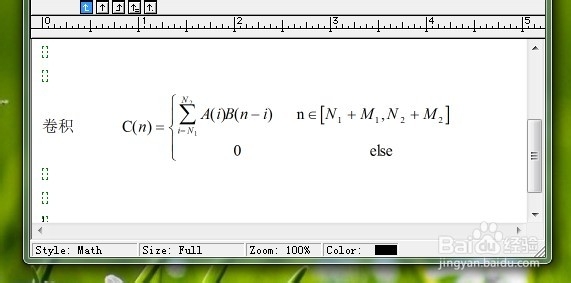2/3

相关函数指令

Matlab中的conv和deconv指令不仅可以用于多项式的乘除运算，还可以用于两个有限长序列的卷积和解积运算。

Matlab提供的函数conv，语法格式：w=conv(u，v)，其中u和v分别是有限长度序列向量，w是u和v的卷积结果序列向量。如果向量u和v的长度分别为N和M，则向量w的长度为N+M-1.如果向量u和v是两个多项式的系数，则w就是这两个多项式乘积的系数。下面我们看一下deconv指令。功能：求向量反褶积和进行多项式除法运算。语法格式：=deconv(v,u) ，参数q和r分别返回多项式v除以多项式u的商多项式和余多项式。具体实例请看下一步。

3/3

conv和deconv指令实例

具体实例请看下图，这里我们求多项式(x2+2x+1)与多项式(2x2+x+3)的积，再求积与(x2+2x+1)的商。需要注意的是向量c代表多项式(2x4+5x3+7x2+7x+3)。

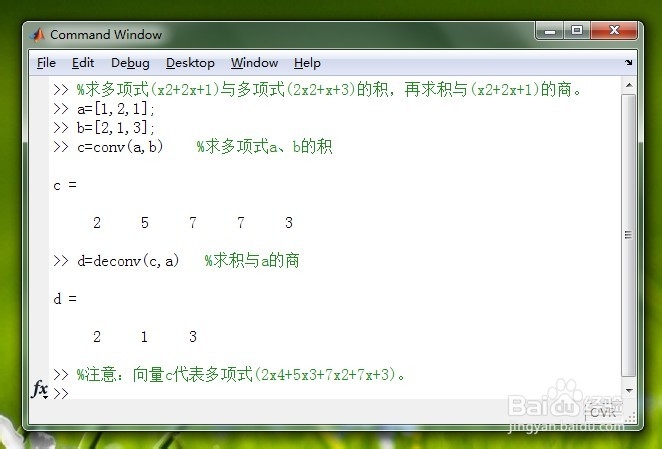两个有限长序列的卷积实例1/6

具体序列的数学形式

在这一步我们将具体的有限长时间序列按数学方式显示，具体请看下图。

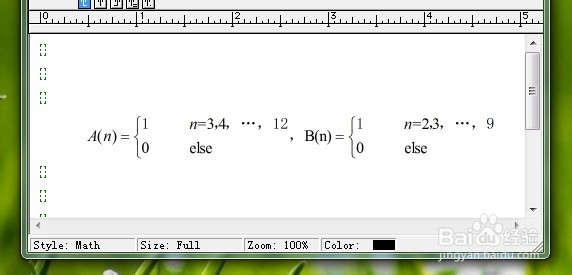2/6

解法一：循环求合法求卷积

在本例中我们将按照原理方法第一步中图二的方式进行卷积计算，即循环求合法求卷积。具体的代码及结果请看下图。图一是是生成有限长度时间序列，图二是根据原理方法第一步中图二的方式即循环求合法求卷积的具体代码，图三是是图二的计算结果。

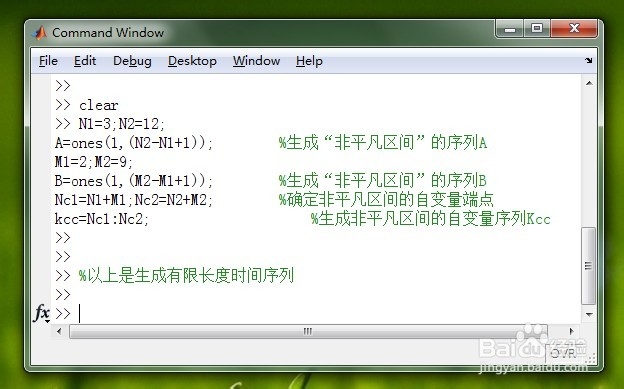
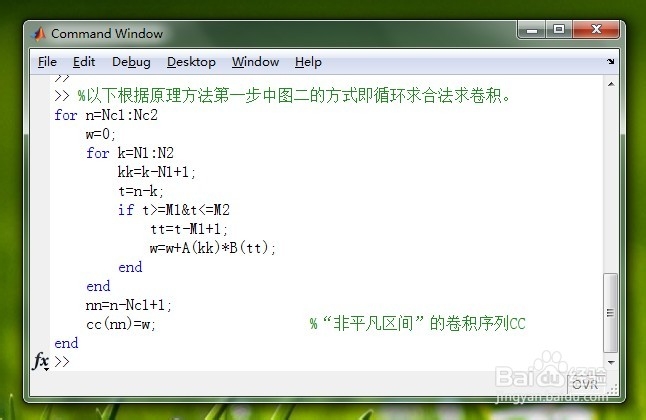
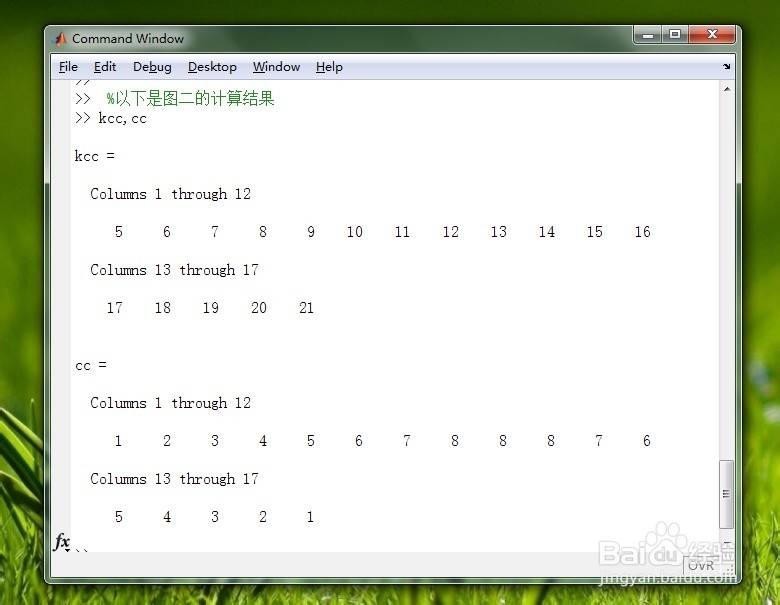3/6

解法二：0起点序列法

下面就说一下第二种方法，即“0起点序列法”，所采用的指令就是我们在原理方法中介绍的conv函数指令。具体代码看下图。

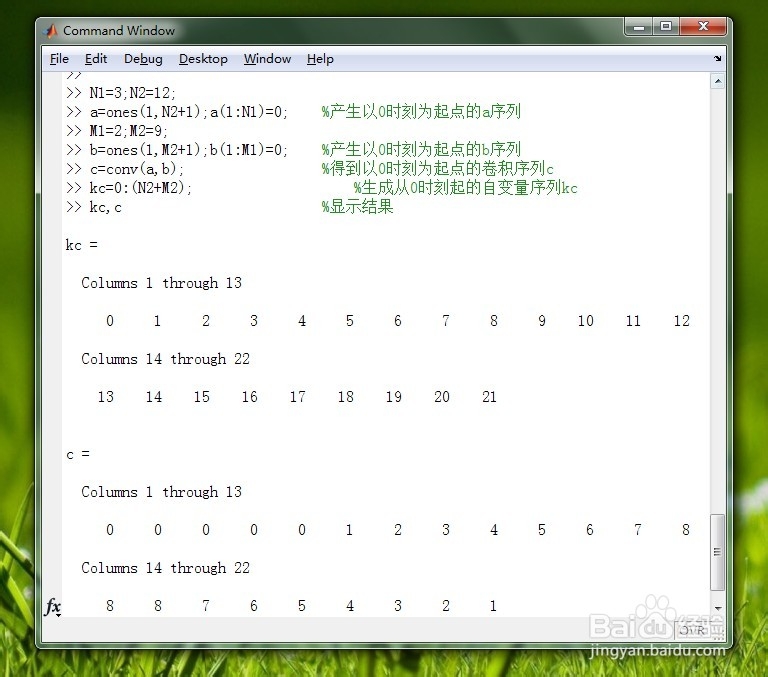4/6

解法三：非平凡区间序列法

下面就说一下第二种方法，即“0起点序列法”，所采用的指令就是我们在原理方法中介绍的conv函数指令。具体代码看下图。图一为计算代码，图二为计算结果。

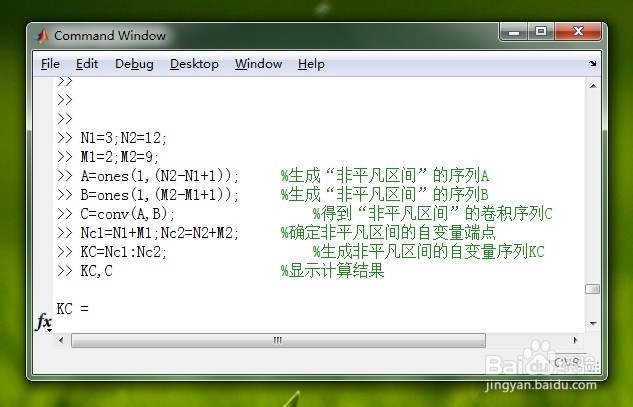
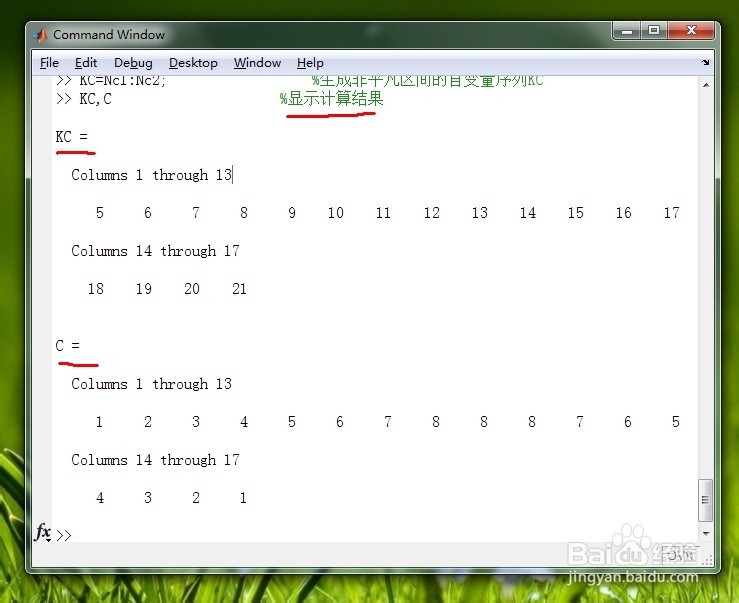5/6

绘图比较

这一步我们将解法二和解法三的计算结果绘制在一张图片中进行比较，其中第一幅是“0起点法”的计算结果图，第二幅是“非平凡区间法”的计算结果图。其中画图代码为：

subplot(2,1,1),stem(kc,c),text(20,6,'0 起点法') %画解法二的结果

CC=; %补零是为了两子图一致

subplot(2,1,2),stem(kc,CC),text(18,6,'非平凡区间法') %画解法三的结果

xlabel('n')

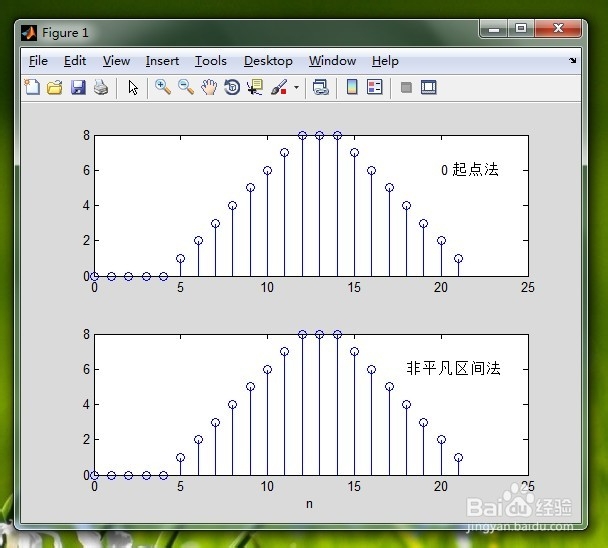6/6

小结

有以上可以得出如下结论：

1、“解法三”最简洁、通用；

2、“解法二”使用于序列起点时刻N1或（和）M1小于0的情况，比较困难；

3、“解法一”最繁琐，效率低下。

注意事项

现在有matlab的中文版本：matlab r2016a，大家可以试试。安装激活教程为：http://jingyan.baidu.com/article/e75057f2f099fcebc91a8906.html

MATLAB卷积