三角形中位线定理：三角形的中位线平行于第三边（不与中位线接触），并且等于第三边的一半。

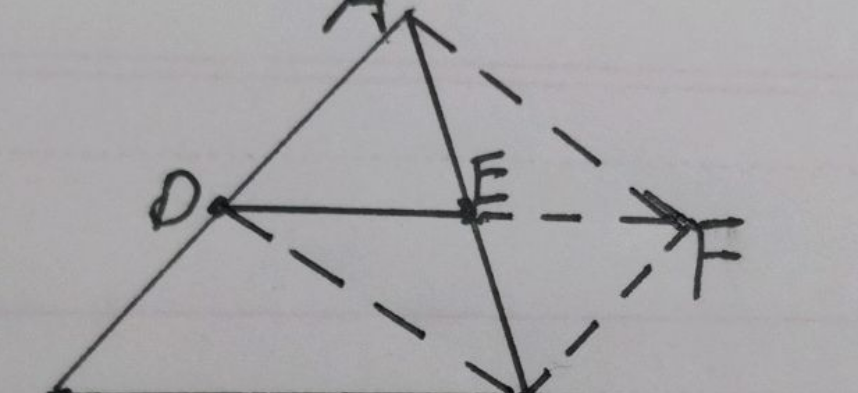
证明：已知△ABC中，D，E分别是AB，AC两边中点。求证DE平行于BC且等于BC/2。

过C作AB的平行线交DE的延长线于G点。

∵CG∥AD。

∴∠A=∠ACG。

∵∠AED=∠CEG、AE=CE、∠A=∠ACG（用大括号）。

∴△ADE≌△CGE（A.S.A)。

∴AD=CG(全等三角形对应边相等）。

∵D为AB中点。

∴AD=BD。

∴BD=CG。

又∵BD∥CG。

∴BCGD是平行四边形（一组对边平行且相等的四边形是平行四边形）。

∴DG∥BC且DG=BC。

∴DE=DG/2=BC/2。

∴三角形的中位线定理成立。

简介：

三角形中位线是三角形中重要的线段，三角形中位线定理是一个重要性质定理，它是前面已学过的平行线，全等三角形，平行四边形等知识内容的应用和深化，对进一步学习非常有用，在判定两直线平行和论证线段倍分关系时常常用到。

在三角形中位线定理的证明及应用中，处处渗透了化归思想，它是一种重要的思想方法。