【抽象代数】双二次扩域Q[i,sqrt(2)]的分析
来源:网络收集 点击: 时间:2024-07-11【导读】:
本文,理顺一下双二次扩域Q的一些内容。工具/原料more电脑python方法/步骤1/7分步阅读 2/7
2/7 3/7
3/7 4/7
4/7 5/7
5/7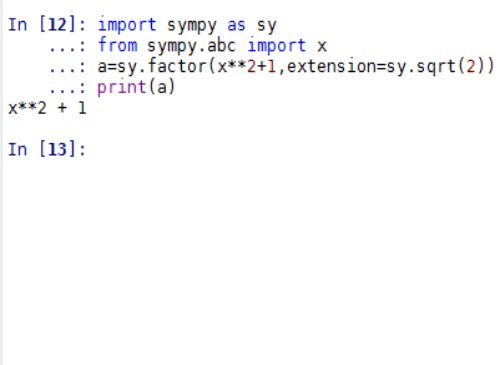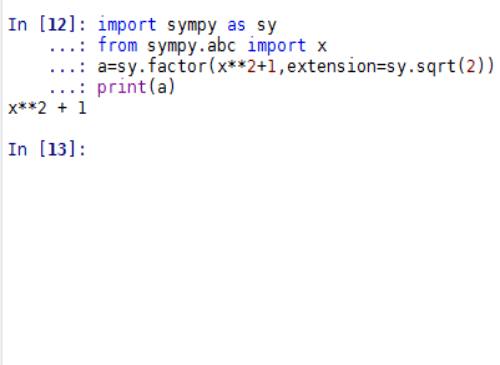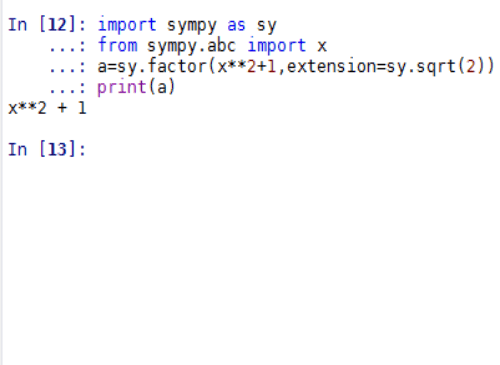 6/7
6/7 7/7
7/7
Q是从有理数域Q扩张而来。
这个过程可以分为两步。
 2/7
2/7Q是Q的二次扩域。
 3/7
3/7Q是Q的二次扩域。
 4/7
4/7但是这个二次扩域不是这么来的。
实际上,我们需要证明,x^2-2在Q里面是既约多项式。
这只需要证明它不能分解因式就行了。
证明了x^2-2在Q里面是既约多项式,那么就说明Q是Q的二次扩域,进而说明它是Q的双二次扩域。
 5/7
5/7上面的Q扩张到Q的顺序是:
Q⊂Q⊂Q
我们还可以把扩张顺序颠倒一下:
Q⊂Q⊂Q
为此,我们要证明,多项式x^2+1=0在Q里面是既约多项式。
 6/7
6/7Q的自同构群有四个元素,其中:
σ表示复共轭,它保持sqrt(2)的符号不变;
τ把sqrt(2)变为相反数,而保持i的符号不变;
στ是二者的复合,把i和把sqrt(2)都变为相反数。
这个群同构于Klein四元群。
 7/7
7/7Q的自同构群有三个真子群,分别对应于Q和Q之间的三个中间域。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_948952.html
上一篇:PPT如何把艺术字转换成繁体字
下一篇:小红书app如何隐藏在线状态
 订阅
订阅