在编程的处理数据过程中通常需要定义数组来实现矩阵运算，矩阵的求逆也经常会使用到，那么我们在使用C#时怎么求矩阵的逆呢。工具/原料more电脑，visual studio 2015方法/步骤1/6分步阅读

双击运行visual studio 2015，文件-新建一个项目，可以是窗体也可以是控制台应用程序，看个人的编程题目要求而定。

2/6

定义一个矩阵（数组）a，c#中都是用数组来存储矩阵的，下面就求矩阵a的逆：

double a = new double { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };

3/6

下面我们写一个类来实现矩阵的求逆（也可以写函数求逆），因为类只要调用就行了，而且不在主程序的代码中，可以简化我们的程序。创建方法如下：解决方案资源管理器-项目名称-添加-类。

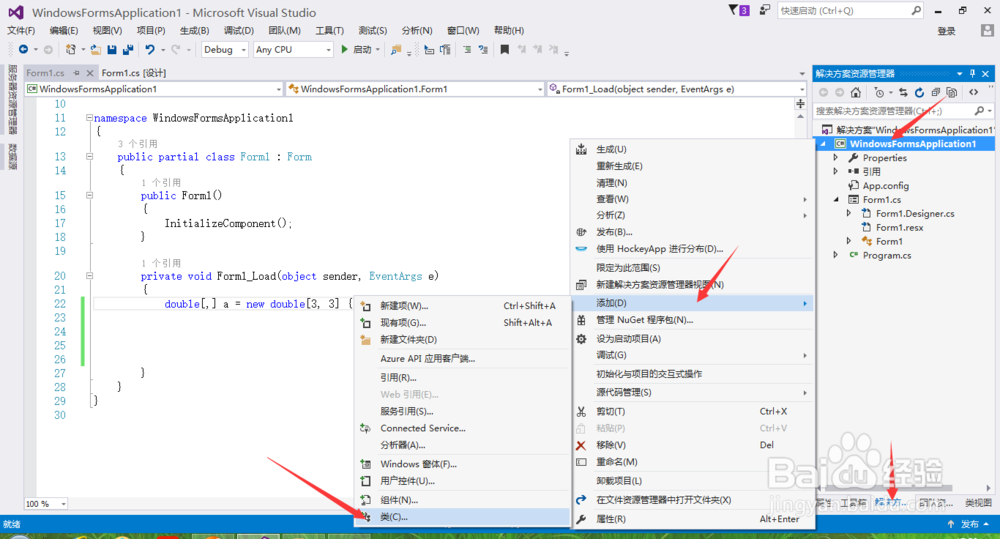4/6

类的名称改为“qiuni”。

5/6

在“求逆”类中添加矩阵求逆的代码（图片只截取了部分，全部代码如下）：

public static double 求逆(double A)

{

int n;

n = A.GetLength(0);

if (n != A.GetLength(1)) return null;

double C = new double;

double D = new double;

for (int i = 0; i n; i++)

for (int j = 0; j n; j++)

C = A;

for (int i = 0; i n; i++)

C = 1;

for (int k = 0; k n; k++)

{

double max = Math.Abs(C);

int ii = k;

for (int m = k + 1; m n; m++)

if (max Math.Abs(C))

{

max = Math.Abs(C);

ii = m;

}

for (int m = k; m 2 * n; m++)

{

if (ii == k) break;

double c;

c = C;

C = C;

C = c;

}

if (C != 1)

{

double bs = C;

if (bs == 0)

{

Console.WriteLine(求逆错误！结果可能不正确！);

break;

//return null;

}

C = 1;

for (int p = k + 1; p n * 2; p++)

{

C /= bs;

}

}

for (int q = k + 1; q n; q++)

{

double bs = C;

for (int p = k; p n * 2; p++)

{

C -= bs * C;

}

}

}

for (int q = n - 1; q 0; q--)

{

for (int k = q - 1; k -1; k--)

{

double bs = C;

for (int m = k + 1; m 2 * n; m++)

{

C -= bs * C;

}

}

}

for (int i = 0; i n; i++)

for (int j = 0; j n; j++)

D = C;

return D;

}

6/6

最后，回到主程序，定义矩阵（数组）b为a的逆矩阵，并调用我们的“求逆”类，就可以实现对矩阵的求逆运算了：

学习逆矩阵